Priority Queue（优先队列）

2021-03-08

0. 相关文章

1. Priority Queue 优先队列

Recap: Queue 的特点是 FIFO（先进先出）。

Reference: https://runestone.academy/runestone/books/published/pythonds3/Trees/TreeTraversals.html (7.7 - 7.10)

Priority Queue 是 Queue 的一个变体，和 Queue 相同的地方在于，dequeue（退出队列）的时候是从最前面开始 remove item。

和 Queue 不同的地方在于，队列里面的 item 是根据逻辑顺序而非时间顺序来排列的，逻辑顺序由 item 的优先级决定。

队列最前面是优先级最高的 item，最后面是优先级最低的 item，优先级高的先出。

进入队列（enqueue）的时候，优先级高的 item 也会在靠前的位置。

优先队列是一个数据结构，有助于实现一些 graph algorithm。

如何实现优先队列？

最简单的方法：用 sorting function + list 来实现。

时间复杂度：insert - $O(n)$, sort - $O(nlog(n))$

更好的方法：用 binary heap 来实现。

时间复杂度：enqueue - $O(log(n))$, dequeue - $O(log(n))$

2. Binary Heap 二叉堆

Binary Heap 看起来很像树结构，但是实际上只需要一个 list 来实现。

Binary Heap 有两个常见的变体：Min Heap（最小堆）和 Max Heap（最大堆）。

Min Heap: 最小的在最前

Max Heap：最大的在最前

Binary Heap 的常见功能（以 Min Heap 为例）

create, insert(k), get_min, delete, is_empty, size, heapify(list)

heapify 是把一个 list 变成 Binary Heap 的 function。

如何实现 Binary Heap

为了实现 $log(n)$ 的时间复杂度，我们可以用 binary tree（二叉树）来代表我们的 heap，并且通过让二叉树保持平衡来达到 $log(n)$ 的时间复杂度。

A balanced binary tree has roughly the same number of nodes in the left and right subtrees of the root.

$log(n)$的时间复杂度跟保持平衡有啥关系？

$log(n)$是 $log_2(n)$ 的简写，保持平衡意味着树的高度是 item 数量的一半（x/2），也就实现了 enqueue 和 dequeue 这两个操作的 $log(n)$ 时间复杂度（排序时对比的次数减少了一半）。

怎么保持二叉树平衡呢？

通过创建一颗 complete binary tree（完全二叉树），它的特点是每一层都有两个节点（除了最下面一层），每一层都是从左到右来创建节点的（如下图）。

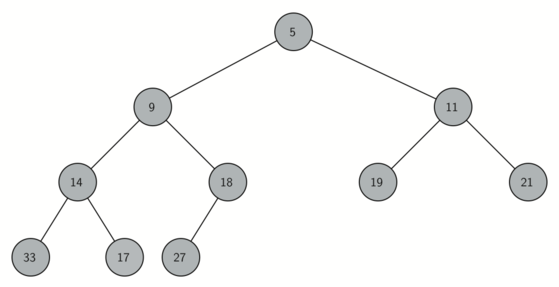
如何只用一个 list 来代表 complete binary tree 呢？

我们不需要用 list of list 来代表上面的树结构，也不需要 node 和 reference。

因为这是完全二叉树，每个 parent 都有两个 child（除了最底层），所以任何一个 parent node (index = p) 左边的 child node index 都可以通过 2p + 1 来计算，同理，右边的 child node index = 2p + 2。

假如给定一个 node index = n，需要找到 parent node index，那我们就可以通过 (n-1)//2 来计算。

比如上面那棵树，就可以用这个 list 来表示：5, 9, 11, 14, 18, 19, 21, 33, 17, 27 （从上到下，从左到右）

19 的 index = 5, parent node index = (5-1)//2 = 2, parent node = 11。

9 是 parent node，index = 1，9 的左 child node index = 2+1 = 3，左 child node = 14，右 child node index = 2+2 = 4，右 child node = 18。

用 list 表示 complete binary tree 的好处是什么？

我们可以高效地去实现 binary heap 这个数据结构，降低 operation 的时间复杂度。

Min Heap Order

堆的 item 顺序是非常重要的，因为最小堆要保证 min value 在最前面，所以我们要遵循这个原则：

对于 parent node 的每个 child node ，parent key ≤ child key。

这样一来，root node 就一定是最小的值。

Min Heap Implementation

Insertion 逻辑

把新的 item 放在 list 最后，然后根据公式找到它的 parent，去跟 parent 比较大小，假如小于 parent，就和 parent 互换位置，然后继续比较，直到和 root 比完为止；

Deletion 逻辑

把 root 移除之后，把最后一个 item 放到 root 的位置；
然后新的 root 去跟 child node 进行比较，假如大于 child 就互换位置，直到位置正确为止。

Heapify 逻辑

假如从头开始建一个 list，把每个 item 一个个插入进去，时间复杂度是 list insertion $O(n)$ + find index O($log(n)$) = O($nlog(n)$)；
更好的方法是：直接建立一个完整的 list，从中间的 item 开始重新排序，_perc_down method 可以保证最大的 item 永远在 list 的后面，这个方法的时间复杂度是 O(n)；

class BinaryHeap:
    def __init__(self):
        self._heap = []

    def insert(self, item):
        self._heap.append(item)
        self._perc_up(len(self._heap) - 1)

    # internal method, used to make sure the order is correct by swapping parent with child when parent > child
    def _perc_down(self, cur_idx):
        while 2 * cur_idx + 1 < len(self._heap):
            min_child_idx = self._get_min_child(cur_idx)
            if self._heap[cur_idx] > self._heap[min_child_idx]:
                self._heap[cur_idx], self._heap[min_child_idx] = (
                    self._heap[min_child_idx],
                    self._heap[cur_idx],
                )
            else:
                return
            cur_idx = min_child_idx

    def _get_min_child(self, parent_idx):
        if 2 * parent_idx + 2 > len(self._heap) - 1:
            return 2 * parent_idx + 1
        if self._heap[2 * parent_idx + 1] < self._heap[2 * parent_idx + 2]:
            return 2 * parent_idx + 1
        return 2 * parent_idx + 2

    def delete(self):
        self._heap[0], self._heap[-1] = self._heap[-1], self._heap[0]
        result = self._heap.pop()
        self._perc_down(0)
        return result

    # use _perc_down to ensure large item is after small item
    def heapify(self, not_a_heap):
        self._heap = not_a_heap[:] # deep clone
        cur_idx = (len(self._heap) - 1) // 2 # find middle item index
        while cur_idx >= 0:
            self._perc_down(cur_idx)
            cur_idx = cur_idx - 1 # out of loop when len(self._heap) = 0

    def is_empty(self):
        return not bool(self._heap)

    def __len__(self):
        return len(self._heap)

    def __str__(self):
        return str(self._heap)

a_heap = BinaryHeap()
a_heap.heapify([9, 5, 6, 2, 3])

while not a_heap.is_empty():
    print(a_heap.delete())

如何证明我们可以用 O(n) 的时间复杂度来进行 heapify？

The key to understanding that you can build the heap in 𝑂(𝑛) is to remember that the log𝑛 factor is derived from the height of the tree. For most of the work in heapify, the tree is shorter than log𝑛.

我们之前提到，保持二叉树的平衡可以让树的高度总是小于等于 item 总量的一半，所以 enqueue 和 dequeue 都是 O($log(n)$) 的时间复杂度，这是由树的高度决定的。

而 heapify 的大部分操作都是从中间高度小于 $log(n)$ 的树上面进行的。

Using the fact that you can build a heap from a list in 𝑂(𝑛) time, you will construct a sorting algorithm that uses a heap and sorts a list in 𝑂(𝑛log𝑛).