AVL Tree（二叉平衡查找树）

2021-03-10

前言

AVL tree = Balanced Binary Search Tree

之前我们讲过，二叉查找树的效率是与树的高度相关的，当树变得不平衡时，operation 的时间复杂度可能会增加到 O(n).

这一篇要讲的是一种特殊的二叉查找树，它在任何时候都是平衡的。

This tree is called an AVL tree and is named for its inventors: G.M. Adelson-Velskii and E.M. Landis.

1. AVL Tree

这种树和二叉查找树都实现了Associative Array（Map）ADT，唯一区别是效率。

AVL Tree 需要我们持续追踪每个 node 的 balance factor（平衡因子）。

𝑏𝑎𝑙𝑎𝑛𝑐𝑒_𝑓𝑎𝑐𝑡𝑜𝑟=ℎ𝑒𝑖𝑔ℎ𝑡(𝑙𝑒𝑓𝑡_𝑠𝑢𝑏𝑡𝑟𝑒𝑒)−ℎ𝑒𝑖𝑔ℎ𝑡(𝑟𝑖𝑔ℎ𝑡_𝑠𝑢𝑏𝑡𝑟𝑒𝑒)

这个 factor 是左子树高度 - 右子树高度。

factor > 0, left-heavy;
factor = 0, balanced;
factor < 0, right-heavy

AVL Tree: balance_factor = [-1, 0, 1]

当 balance_factor 超过这个范围时，我们就要让树重新变得平衡。

树里面节点的数量和树的高度之间的关系$h (𝑁_ℎ)$可以用这个算式来表示：

$𝑁_ℎ$=1+$𝑁_{ℎ-1}$+$𝑁_{ℎ−2}$，类似 Fibonacci sequence 斐波那契数

斐波那契数

F0 = 0
F1 = 1
Fi = $F_{i-1}$ + $F_{i-2}$ for all i >= 2

如何达到平衡？

假如我们要 insert 一个 new node，这个 node 是 leaf node，我们不需要对这个新 node 做什么，但是我们要 update 这个新 node 的 parent node 的 balance factor。如果新 node 是 left child，那么 balance factor 就 + 1；反之 - 1。

Since all new keys are inserted into the tree as leaf nodes and we know that the balance factor for a new leaf is zero, there are no new requirements for the node that was just inserted.

这个是适用于 grandparent 以及更高 level 的 recursive 变动。

recursive call 到达了 root；
balance of parent = 0 （grandparent 的 balance 不变）

Since this is a recursive procedure let us examine the two base cases for updating balance factors:

The recursive call has reached the root of the tree.

The balance factor of the parent has been adjusted to zero. You should convince yourself that once a subtree has a balance factor of zero, then the balance of its ancestor nodes does not change.

2. Code

AVL Tree 是 BinarySearchTree 的subclass
Override _put，使用 update_balance

def _put(self, key, value, current_node):
    if key < current_node.key:
        if current_node.left_child:
            self._put(key, value, current_node.left_child)
        else:
            current_node.left_child = AVLTreeNode(
                key, value, 0, parent=current_node
            )
            self.update_balance(current_node.left_child)
    else:
        if current_node.right_child:
            self._put(key, value, current_node.right_child)
        else:
            current_node.right_child = AVLTreeNode(
                key, value, 0, parent=current_node
            )
            self.update_balance(current_node.right_child)

def update_balance(self, node):
    if node.balance_factor > 1 or node.balance_factor < -1:
        self.rebalance(node)
        return
    if node.parent:
        if node.is_left_child():
            node.parent.balance_factor += 1
        elif node.is_right_child():
            node.parent.balance_factor -= 1

        if node.parent.balance_factor != 0:
            self.update_balance(node.parent)

3. 如何有效地达到平衡？—— 旋转

Efficient rebalancing is the key to making the AVL Tree work well without sacrificing performance. In order to bring an AVL Tree back into balance we will perform one or more rotations on the tree.

旋转的具体步骤

在 A node 做一次左旋：

把右 child (B) 提升为 root node（取代A的位置）；
把 A 变成新 root node 的左 child；
假如 B 本来就有左 child，那么 A 取代左 child，原来的左 child 变成 A 的右 child（因为 B 原来是 A 的右 child，所以 A 的右 child 必定为空）；

在 E node 做一次右旋：

把左 child（C）提升为 root node（取代E的位置）；
让 E 变成新 root node 的右 child；
假如 C 本来就有个右 child（D），那么这个右 child（D）成为新右 child（E）的左 child（因为 C 本来是 E 的左 child，所以 E 的左 child 必定为空）；

Code


def rotate_left(self, rotation_root):
    new_root = rotation_root.right_child
    rotation_root.right_child = new_root.left_child
    # adjust the parent pointers of the two nodes
    if new_root.left_child:
        new_root.left_child.parent = rotation_root
    new_root.parent = rotation_root.parent
    if rotation_root.is_root():
        self._root = new_root
    else:
        if rotation_root.is_left_child():
            rotation_root.parent.left_child = new_root
        else:
            rotation_root.parent.right_child = new_root
    new_root.left_child = rotation_root
    # set the parent of the old root to be the new root.
    rotation_root.parent = new_root
    # 接下来会证明这个公式
    rotation_root.balance_factor = (
        rotation_root.balance_factor + 1 - min(new_root.balance_factor, 0)
    )
    new_root.balance_factor = (
        new_root.balance_factor + 1 + max(rotation_root.balance_factor, 0)
    )

4. 如何更新 balance factor？

我们需要计算old root 和 new root 的 balance factor。

每个subtree的高度用$h_x$来表示。

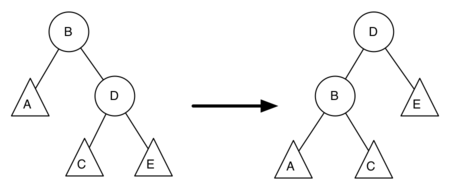
已知：

old_bal(B) = $h_A - h_D$ = 1 - 2 = -1

new_bal(B) = $h_A - h_C$ = 1 - 1 = 0

$h_D = 1 + max(h_C, h_E)$ // height of D is 1 + the maximum height of its children

证明：

new_bal(B) = 𝑜𝑙𝑑_𝑏𝑎𝑙(𝐵)+1−𝑚𝑖𝑛(0,𝑜𝑙𝑑_𝑏𝑎𝑙(𝐷))

步骤：

改写 old_bal(B) 的公式

old_bal(B) = $h_A - h_D$ = $h_A - (1 + max(h_C, h_E))$
new_bal(B) - old_bal(B)

= $h_A - h_C - (h_A - (1 + max(h_C, h_E)))$

= $h_A - h_C - h_A + (1 + max(h_C, h_E))$

= $h_A - h_C - h_A + 1 + max(h_C, h_E)$

= $1 + max(h_C, h_E) - h_C$

= $1 + max(h_C - h_C, h_E - h_C)$ # Note: $𝑚𝑎𝑥(𝑎,𝑏)−𝑐=𝑚𝑎𝑥(𝑎−𝑐,𝑏−𝑐)$
new_bal(B)

= $1 + max(h_C - h_C, h_E - h_C)$ + old_bal(B)
因为 $h_E - h_C$ = -old_bal(D)，且 $𝑚𝑎𝑥(−𝑎,−𝑏)=−𝑚𝑖𝑛(𝑎,𝑏)$
new_bal(B) = old_bal(B) + 1 + max(0, -old_bal(D))

= old_bal(B) + 1 - min(0, old_bal(D))

= old_bal(B) + 1 - min(old_bal(D), 0) # Note: min 里面顺序无所谓

所以刚才那段 rotate_left 的代码是正确的。

# old_bal(B) = rotation_root.balance_factor
# old_bal(D) = new_root.balance_factor
# 最后的结果是 new_bal(B), assign to rotation_root.balance_factor
rotation_root.balance_factor = (
  rotation_root.balance_factor + 1 - min(new_root.balance_factor, 0)
)

# 计算 new_bal(D)
# old_bal(D) = new_root.balance_factor
# new_bal(B) = rotation_root.balance_factor
# 这个算式也可以用类似的方法推出来。
new_root.balance_factor = (
  new_root.balance_factor + 1 + max(rotation_root.balance_factor, 0)
)

5. 一种特殊情况

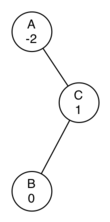
这种不平衡的情况是没法通过左旋来解决的。

假如 C 成为新 root，A 成为 C 的左 child，B 成为 A 的右 child，结果还是不平衡的。

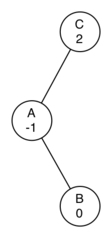
怎么办？？

在发现不平衡之后，不要简单地根据 balance factor < -1 来决定现在要进行左旋。

我们应该先看一下右 child 的 balance factor，假如 > 0 的话我们要先对这个 child 做一次右旋，然后再对它的 parent node 做左旋（如下图所示）。

A 的 balance factor 是 -2，我们需要左旋，但是 A 的右 child（C）的 balance factor 是 1（左重右轻），此时我们应该先把 C 进行右旋。
C 的右旋步骤：先把 B 提上来，然后再让 C 成为 B 的右 child
最后我们就可以进行 A 的左旋了

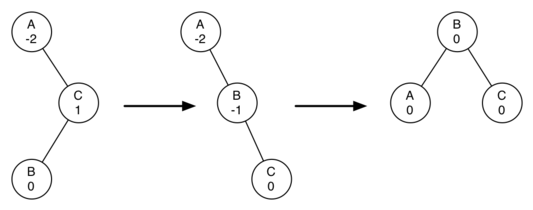
同理适用于 parent node 的右旋（先 check 左 child）。

def rebalance(self, node):
    if node.balance_factor < 0:
        if node.right_child.balance_factor > 0:
            self.rotate_right(node.right_child)
            self.rotate_left(node)
        else:
            self.rotate_left(node)
    elif node.balance_factor > 0:
        if node.left_child.balance_factor < 0:
            self.rotate_left(node.left_child)
            self.rotate_right(node)
        else:
            self.rotate_right(node)

结语

通过让二叉树保持平衡，我们可以保证 get method 的时间复杂度是 $O(log_2(n))$，因为树的高度永远是(node总数-1)的一半。

put method 有两个步骤：

第一步是把新 node 插入树，成为一个 leaf node，

然后再更新所有 parent node 的 balance refactor，更新最多需要 $log_2(n)$ 次，每一个 level 一次。

完成更新之后，假如树不平衡了，那么我们最多需要旋转两次就可以把树变回平衡状态。

每次旋转的时间复杂度是 O(1)，所以整个 put 的时间复杂度是 2*1 + $log_2(n)$ ≈ $log_2(n)$