两种常见的 Graph 实现方式
2021-04-27
0. Graph ADT
这个抽象数据结构需要有以下方法:
Graph()addVertex(vert)- 在图里加入一个 nodeaddEdge(fromVert, toVert)- 加一个连接两个node的单向 edgeaddEdge(fromVert, toVert, weight)- 加一个连接两个node的单向 edge,带有重量属性getVertex(vertKey)- 根据 node key 找到 nodegetVertices()- 返回全部的 node (list)vertex in graph- 确认存在与否,根据情况返回 True 和 False
两种常见的 Graph implementation 是 Adjacency Matrix(邻接矩阵)和 Adjacency List(邻接表)。
1. Adjacency Matrix(邻接矩阵)
| V0 | V1 | V2 | |
|---|---|---|---|
| V0 | 5 | ||
| V1 | 4 | ||
| V2 | 2 |
用一个二维矩阵来代表 Graph,在表格中的行和列代表node,比如V0,V1,有数字的 cell(如 V0 和 V1 的 5) 就代表它的所在行 node(V0)和它的所在列 node(V1)之间有一条 edge,当两个 node 被 edge 连接起来的时候,我们就说它们是 adjacent(邻接的),cell 里面的数字(5)就代表这条 edge 的 weight。
邻接矩阵可以让我们用一个表格来代表 node 之间的关系以及 edge 的相关信息。
邻接矩阵的好处在于它是非常简单的,假如 node 数量不多,你可以很容易地看到 node 之间的联系。
邻接矩阵的缺陷
不过这个表格里面大部分的 cell 都是空的(浪费啊!!),所以我们认为这个邻接矩阵是 sparse(稀少的)。也就是说,矩阵并不是用来存稀少数据的一种有效率的选项。
在 Python 中,你必须付出额外的努力才能创造这样的一个”稀少“矩阵结构。
那么这个邻接矩阵在什么时候适合使用呢?
当这个矩阵里面大部分的 cell 都是有数值的,也就是大部分 node 之间都有连接的时候。
假如所有的 node 都有连接,那么矩阵里面的 edge 数量就等于 V*V = V^2,但是这种情况很少见,所以我们接下来要讨论的是「稀少矩阵」的情况。
A matrix is full when every vertex is connected to every other vertex. There are few real problems that approach this sort of connectivity.
2. Adjacency List(邻接表)
刚才我们提到了邻接矩阵的缺点(空间利用效率低),下面就介绍一个能更好地利用空间的方法来实现 Graph —— 邻接表。
这个方法是这样的:
- 创建并维护一个包含所有 node 的 master list —— 代表 graph;
- 每个 node 都有一个自己的 list,这个 list 里面包含所有和它相连接的 node 以及 edge 信息;
这个信息用 dictionary 来表示,key 就是 node,value 是 weight,如:{V1:5, V2:4}
所以 node 本身也是一个 dictionary,比如
{ id:"V0", adj:{V1:5, V2:4} }
大概的图就是这样的(来源于runestone教程 )
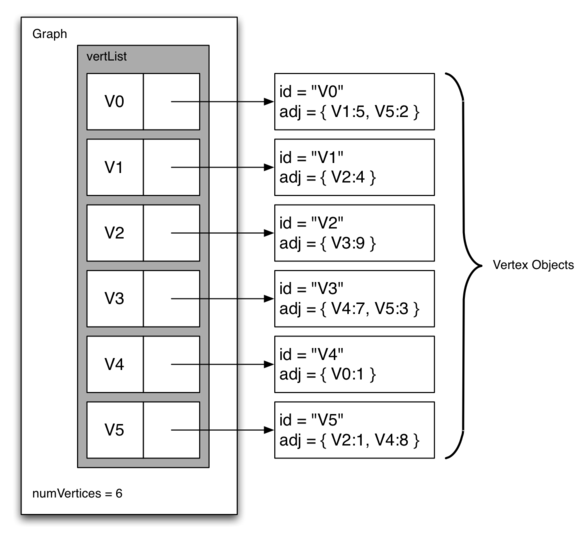
邻接表的好处
更高效的使用空间来代表一个「稀少矩阵」/「稀少图」,并且我们根据一个 node 就能找到所有和它相关的信息。