Graph: The Word Ladder Problem (1)
2021-04-29
0. 前言
Word Ladder 是一个解密游戏,1878 年由爱丽丝漫游奇境的作者 Lewis Carroll 发明。
目标:假设我们要把"FOOL"这个单词转成"SAGE"。
规则:我们需要一个一个字母进行替换,每一次替换都要保证整个单词还是一个有效的单词(比如不能把 FOOL 变成 AOOL 这种完全没有意义的组合)。
示例: FOOL POOL POLL POLE PALE SALE SAGE
加强版:必须要在规定的次数里面完成词汇变形,或者必须要用到某个单词。
跟 Graph 有什么关系呢?
我们的目标是:用最少的次数完成词汇变形。
怎么做?
- 先用 graph 来表示词汇之间的关系,每个词是一个 node,两个词如果只有一个字母不同,就连起来;
- 再用一个叫做 breadth first search 的 graph 算法来找到从 starting word 到 ending word 的最短路径。
1. 创建 Word Ladder Graph
Step 1: 思考这个 graph 的属性是什么
- undirected,fail 和 fall 之间有联系,但可以相互转换,没有方向的限制;
- edge unweighted,edge 不需要有重量的属性。
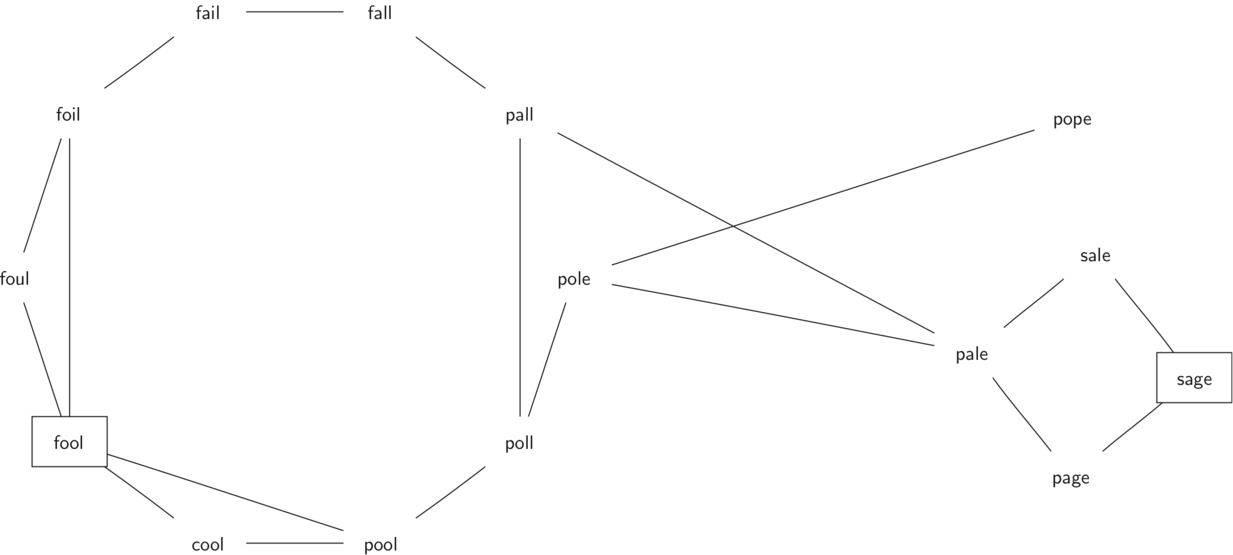
Step 2: 创建 Graph
方法 1
- 先假设我们有一个 word list,里面每个词的长度都相等;
- 然后根据每个词创建 node;
- 通过比较每两个词之间的区别,来找到词汇之间的联系(比较的时候要知道多少个字母不同);
这个方法对于比较小的 word list 来说还算 ok,但是假如你的词汇表有好几千好几万个词,那效率就很低了。
最后一步比较的时间复杂度 = O(n^2),因为是两个 for loop 来进行比较。
方法 2
我们用分组法来处理词语,如下图,保持一个字母的随机性以及其他字母的固定性。
这样一来,我们可以根据词语的长度来分成不同的 buckets,4个字符长的词语就有 4 个 bucket。通过使用 wildcard(通配符),我们可以把 POPE 和 ROPE 都放进 _OPE 这个 bucket 里面。
Note: POPE 也会被放进 P_PE, PO_E, POP_这些小组,也就是每个词语会逐一跟 4 个 bucket 对比。
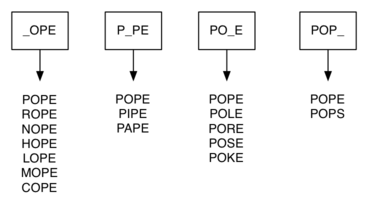
我们可以用 dictionary 来实现这个方法,_OPE 就是 key,匹配的词汇就是 value(一个 list)。
每个词语都是一个 Node,然后我们把所有在一个 key 里面的 node 都加上 edge(因为它们都有联系)。
这样我们就能通过 dictionary 分组法来构造 graph 啦~
方法 2 代码
class Node:
def __init__(self,key):
self.id = key
self.connectedTo = {}
def addNeighbor(self,neighbourId,weight=0):
self.connectedTo[neighbourId] = weight
def __str__(self):
return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
def getConnections(self):
return self.connectedTo.keys()
def getId(self):
return self.id
def getWeight(self,neighbourId):
return self.connectedTo[neighbourId]
class Graph:
def __init__(self):
self.nodeList = {}
self.numNodes = 0
def addNode(self,key):
if key not in self.nodeList:
self.numNodes = self.numNodes + 1
newNode = Node(key)
self.nodeList[key] = newNode
return newNode
else:
return None
def getNode(self,node):
if node in self.nodeList:
return self.nodeList[node]
else:
return None
def __contains__(self,node):
return node in self.nodeList
def addEdge(self,fromNode,toNode,weight=0):
if fromNode not in self.nodeList:
self.addNode(fromNode)
if toNode not in self.nodeList:
self.addNode(toNode)
self.nodeList[fromNode].addNeighbor(self.nodeList[toNode], weight)
def getNodes(self):
return self.nodeList.keys()
# iteration
def __iter__(self):
return iter(self.nodeList.values())
def buildGraph():
dictionary = {}
graph = Graph()
# create buckets of words that differ by one letter
wordlist = ['POPE', 'ROPE', 'PIPE', 'POPS']
for node in wordlist:
for i in range(len(word)):
bucket = word[:i] + '_' + word[i+1:]
if bucket in dictionary:
dictionary[bucket].append(node)
else:
dictionary[bucket] = [node]
for key, values in dictionary.items() :
for value in values:
print (key, value.id)
# add node and edges for words in the same bucket
for bucket in dictionary.keys():
for word1 in dictionary[bucket]:
graph.addNode(word1)
for word2 in dictionary[bucket]:
if word1 != word2:
graph.addNode(word2)
graph.addEdge(word1,word2)
return graph
print(buildGraph().numNodes)
print(buildGraph().getNodes())
print(buildGraph().getNode('POPE'))
结语
下一篇会讲 Breadth First Search。