0. 前言

Reference: 8.18

搜索引擎（比如 Google）就是把整个互联网看做一个 graph，每个 page 都是 node/vertex，网页上面的超链接就是 edge。

不过呢，我们也都知道，某些网页之间的联系比较密切，有些网页之间就没什么关联，我们很可能会发现，这个互联网 graph 里面有很多 cluster。

You might conclude from this that there is some underlying structure to the web that clusters together web sites that are similar on some level.

那我们要做的就是：找到这些 cluster (Strongly Connected Components)。

帮助我们找 cluster/SCC 的算法叫做 strongly connected components algorithm (SCC).

One graph algorithm that can help find clusters of highly interconnected vertices in a graph is called the strongly connected components algorithm (SCC).

1. Strongly Connected Components (SCC)

定义

strongly connected component - C

C 属于一个 Graph - G

C 需要满足这个条件：在 C 里面的每一对 node（如 v, w），都有 v 到 w 的 edge 以及 w 到 v 的 edge（也就是双向关联）。

下图有三个 SCC，分别用不同的颜色标识出来。

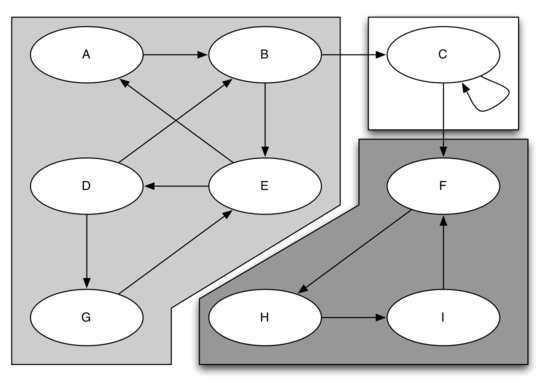
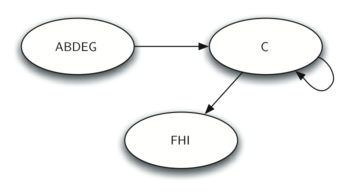
找到 SCC 之后，我们可以用一种简化的方式来表示图（如下）：

2. 概念：Transpose Graph

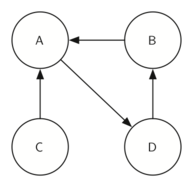
转置就是把所有的 edge 方向换一下，假如 G 里面的 A 到 B 有 edge，那么转置之后的 $G^T$ 就会包含 B 到 A 的 edge。

The transposition of a graph 𝐺 is defined as the graph $𝐺^𝑇$ where all the edges in the graph have been reversed.

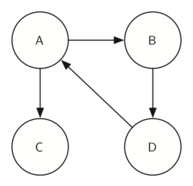
转置前：G

SCC: ABD

转置后 $G^T$

SCC: ABD

3. SCC 步骤

SCC 算法用来计算 graph 里面的 SCC，它基于我们之前讲过的 DFS。

步骤

1. 在 G 里面调用 dfs function，计算每个 node/vertex 的 finishing time；
2. 计算 $G^T$
3. 在 $G^T$ 里面调用 dfs function，但是 DFS 最主要的那个 loop 是以 desceding order of finish time 来遍历 node/vertex 的；
4. Step 3 的结果是一个 forest，这个 forest 里面的每棵树都是 SCC，我们最终输出在 forest 里面的每棵树的每个 node 的 id（一个 list），用来标识 SCC。

图解步骤

0. Graph

1. 计算 G 的 start & finish time

不是很懂实线和虚线的区别，暂且认为它们是一个意思。

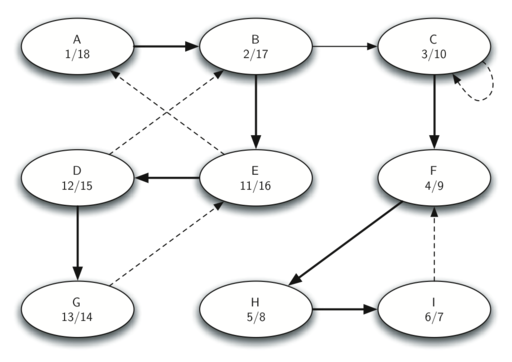
2. 计算 $G^T$ 的 start & finish time

这步之前要先进行 Graph 转置，得到 $G^T$。

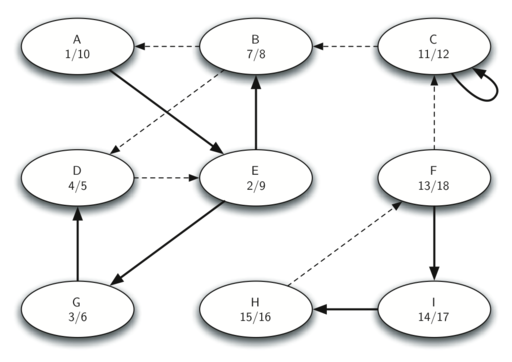
3. Forest of SCC

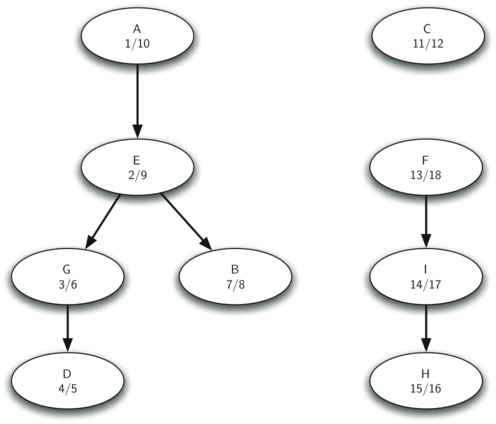
思考

为什么要转置？

https://en.wikipedia.org/wiki/Transpose_graph

Although there is little difference mathematically between a graph and its transpose, the difference may be larger in computer science , depending on how a given graph is represented. For instance, for the web graph , it is easy to determine the outgoing links of a vertex, but hard to determine the incoming links, while in the reversal of this graph the opposite is true. In graph algorithms , therefore, it may sometimes be useful to construct the reversal of a graph, in order to put the graph into a form which is more suitable for the operations being performed on it. An example of this is Kosaraju’s algorithm for strongly connected components , which applies depth first search twice, once to the given graph and a second time to its reversal.