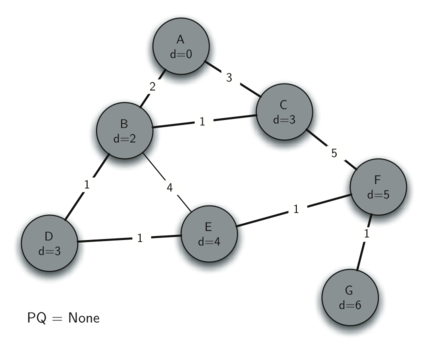
Graph: Prim's Spanning Tree Algorithm
2021-05-13
0. 前言
最后我们再来看一个 Broadcast 问题,有一个broadcast host 在不断发送信息,而所有的 listener 都需要接收到这个信息。比如在线游戏中,所有的玩家都需要知道其他角色的所在位置。
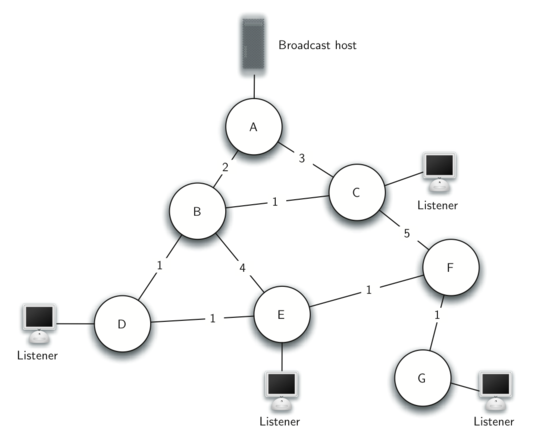
我们可以用一些 brute force 方法(暴力解法)来解决这个问题,我们先来看看怎么暴力解决。
1. 广播问题暴力解法
host 保存一个有所有 listener 的 list,给每个 listener 单独发送信息。
假设发送信息的时候用的是最短路径,那么我们可以计算一下上面这张图的每个 router(就是带字母的 node)被用到了几次。
首先,我们有 4 个 listener,所以一共有 4 个 message copy;
所有的信息先从 host 到了 router A,A 收到 4 个 message。
C 收到一个 message(给 C 边上那个 listener);
B 和 D 会收到 3 个 message,因为它们所在的路径到达其他的 listener 更短……
暴力解法就是让 router 去决定怎么传信息。
Uncontrolled flooding 就是这样一个解法。
Uncontrolled flooding
-
每个 message 都有一个
ttl值(time to live value),这个值被设为大于等于「host 到最远的 listener 的 edge 数量的值」。 -
每个 router 都把 message copy 传给所有的 neighbouring routers;
-
当 message 被传递的时候减少
ttl的值; -
每个 router 继续给 neighbour 发送 message copy 直到
ttl的值为 0;
这种方法毫无疑问会生成很多的无效信息,浪费资源。
2. Prim’s Spanning Tree Algorithm
一个更好的解法需要我们先构建一个 minimum weight spanning tree(最小生成树),目标是每个 node 都只接收一次 message,所有的 listener 都只接收一次信息。
假设我们有一个图:G = (V, E)
Minimum weight spanning tree:T
T 是 E 的一个 acyclic 子集,这个子集里面的 edge 可以连接所有 node/vertice,T 里面 edge 的总和越小越好。
The sum of the weights of the edges in T is minimized.
Directed acyclic graph (DAG):有向无环图
Prim’s algorithm 属于一个算法大类,叫做 “greedy algorithm”(贪心算法),因为每一步我们都会选择 cheapest next step(也就是follow the edge with the lowest weight)。
逻辑
While T is not yet a spanning tree Find an edge that is safe to add to the tree Add the new edge to T
这里的重点是找到 safe edge,什么是 safe edge 呢?
safe edge 就是任何一个能把不在 spanning tree 里面的 node 和在 spanning tree 里面的 node 连起来的 edge。
为什么要找 safe edge 呢?
这能保证我们的 tree 一直是个 tree,也就是没有形成闭环。
We define a safe edge as any edge that connects a vertex that is in the spanning tree to a vertex that is not in the spanning tree. This ensures that the tree will always remain a tree and therefore have no cycles.
Code
这个代码和 Dijkstra’s algorithm 的类似之处在于,它们都用 priority queue 来选择下一个加入 growing graph 的 node/vertex。
规则:只有当一个 node 被移出 priority queue 的时候才能被加入到 spanning tree。
from pythonds.graphs import PriorityQueue, Graph, Vertex
def prim(G,start):
pq = PriorityQueue()
for v in G:
v.setDistance(sys.maxsize)
v.setPred(None)
start.setDistance(0)
pq.buildHeap([(v.getDistance(),v) for v in G])
while not pq.isEmpty():
currentVert = pq.delMin()
for nextVert in currentVert.getConnections():
newCost = currentVert.getWeight(nextVert)
if nextVert in pq and newCost<nextVert.getDistance():
nextVert.setPred(currentVert)
nextVert.setDistance(newCost)
pq.decreaseKey(nextVert,newCost)
3. 图解最小生成树
0. Initialization
A 是 starting node,所有 node 的 dist 都设为 inifinity(无限大),加入 priority queue(以 dist 为 priority)。

1. Router A 接收到 message copy,传给 B
A 的两个邻接 node (B 和 C)的 dist 可以 update 成一个真实的值,因为我们知道 A 到 B 和 A 到 C 的 edge weight。
所以 B 的 dist = 2,C 的 dist = 3。
B 和 C 成为 priority queue 最前面的 node。
然后我们把 B 和 C 的 predecessor link update 成 A。
现在 B 和 C 还没有被加入 spanning tree(因为它们还在 PQ 里面)。
A node is not considered to be part of the spanning tree until it is removed from the priority queue.
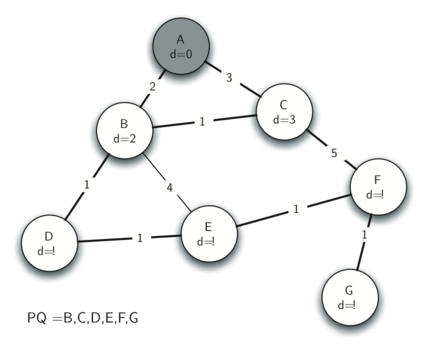
2. Router B 把 message forward 到 D
我们发现 B 的邻接 node (D 和 E)的 dist 也可以被 update。
D dist = 1,E dist = 4。
我们把 message 传给 D,同时 update D 和 E 的 predecessor(指向 B)。

3. Router C
C dist = 3,成为下一个 node。
C 的邻接 node 是 F,F dist = 8。
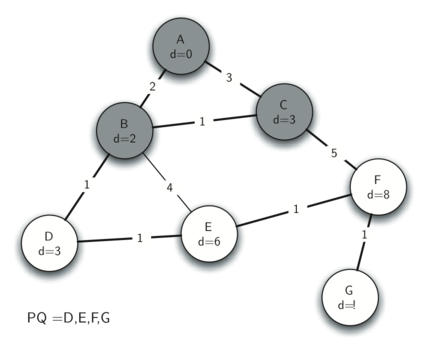
4. Router D
E dist 从 6 减少到 4(A - B - D - E)。
update E 的 predecessor link (指向 D),这样它就可以被加入到 spanning tree 里面了。
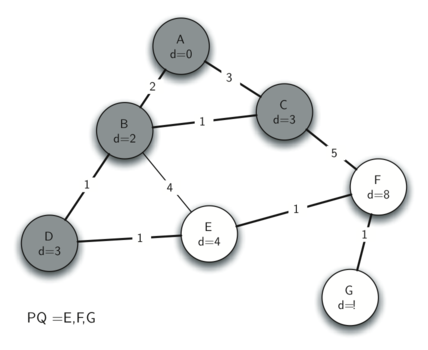
5. Router E
邻接 node 是 F,F 的距离减少到 5,update predecessor 指向 E。
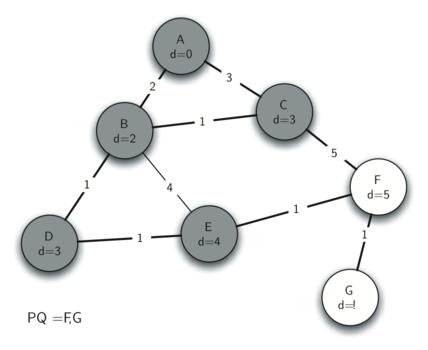
6. Router F
邻接 node 是 G,update G dist = 6,update G predecessor = F。
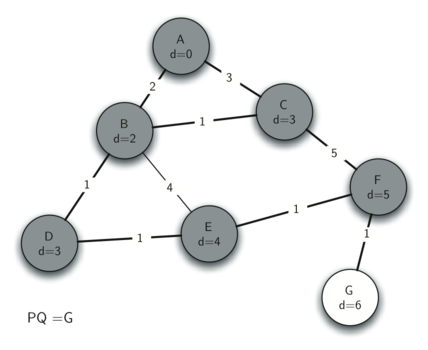
7. Router G
PQ = None,结束~