0. 前言

Reference: 9.1 - 9.2

这章我们会更进一步地讲解之前学过的概念，包括：

1. 如何实现 linked list；
2. 理解 RSA 算法，它被用于 public key encryption，用到了 recursive；
3. 理解另一个 dictionary 的实现方法 - skip list - 的一些特点；
4. 理解 OctTrees 以及在图像处理中的应用；
5. 理解 string-matching 是一个 graph problem；

1. Python Lists

我们之前学了如何用 node 和 reference pattern 来实现 linked list，但是这种实现方法的 Big O 跟 python 自带 list 的 Big O 还是有点差距的，所以这章我们就来看一下 python list 的实现原则（我们没法还原 python 的实现，因为它是用 C 来写的）。

The idea in this section is to use Python to demonstrate the key ideas, not to replace the C implementation.

Key data type: array

list 的实现中，最重要的就是对 array 的使用，这里的 array 是 fixed length，只能存一种类型的数据，只支持两种操作：indexing and assignment to an array index.

举例：

可以把计算机的内存想象成 array，它是一个 continuous block of bytes，这个 block 被分成了 n-byte chunks (n 是根据 array 里面存储的数据类型来决定的)。

比如 python 中的每个 floating point number 都是 16 bytes，下图的 array 就是 16*6 = 96 bytes，base address 是 array 开始的 memory location。

You have seen addresses before in Python for different objects that you have defined. For example: <__main__.Foo object at 0x5eca30> shows that the object Foo is stored at memory address 0x5eca30.

这个 base address 非常重要，因为 index operator 是用一个非常简单的计算完成的：

item_address = base_address + index * size_of_object

假设我们的 array 从 0x000040 开始，想要找到 index = 4 的 object 的地址，我们只需要计算 64 + 4*16 = 128，这个计算的复杂度 = O(1)。

内存地址通常是用 16 进制编码，16进制的0x000040 = 10进制的64。

超出边界

Array 是 fixed size，但是有些编程语言在进行 array 操作的时候并不 check size（比如 C），还有些语言则给出一些很模糊的错误信息。

In the Linux operating system, accessing a value that is beyond the boundaries of an array will often produce the rather uninformative error message “segmentation violation.”

General Strategy of Python Linked List Implementation Using Array

1. Python 用的 array 里面存的是 object reference（也就是 C 里面的 pointer）；
2. Python 用的是一个叫做 over-allocation 的策略，也就是给这个 array 分配比需要的空间更多的空间（allocate an array with space for more objects than is needed initially）；
3. 当 initial array filled up 之后，会 over-allocate 一个更大的 array，并且把之前 array 里面的内容都 copy 到新的 array；

2. Code

Python 没有 array data type，所以我们用 list 来模拟 array.

Constructor

• max_size -> size of current array
• last_index -> keep track of the current end of the list
• my_array -> create a 0 element array
• size_exponent ->

Append

• 先 check 条件：last_index > (max_size - 1)

  假如 true，那么需要一个更大的 array（call _resize）

• 新的 value 加入 last_index 这个位置，然后 last_index + 1

Resize

• __resize means it’s a private method
• 当一个新的 array 被分配好之后，旧的 array 里面的值需要被 copy 到新 array（一个for loop）
• 然后 update max_size 和 last_index，并且增加 size_exponent
• 新 array 被 assign 给 self.my_array
• 在 C 语言中，你要释放旧 array 的空间，但是 python 有 garbage collection，所以我们不用做这一步。

class ArrayList:
    def __init__(self):
        self.size_exponent = 0
        self.max_size = 0
        self.last_index = 0
        self.my_array = []

    def append(self, val):
        if self.last_index > self.max_size - 1:
            self.__resize()
        self.my_array[self.last_index] = val
        self.last_index += 1

    def __resize(self):
        new_size = 2 ** self.size_exponent
        print("new_size = ", new_size)
        new_array = [0] * new_size
        for i in range(self.max_size): 
            new_array[i] = self.my_array[i]

        self.max_size = new_size
        self.my_array = new_array
        self.size_exponent += 1

Resizing strategy

• 这里我们通过 2^size_exponent来计算新的 size

  其他的方法包括乘以1.5，powers of 2 等..

  Python 用 *1.125+constant 来 resize

There are many methods that could be used for resizing the array. Some implementations double the size of the array every time as we do here, some use a multiplier of 1.5, and some use powers of two. Python uses a multiplier of 1.125 plus a constant. The Python developers designed this strategy as a good tradeoff for computers of varying CPU and memory speeds. The Python strategy leads to a sequence of array sizes of 0,4,8,16,25,35,46,58,72,88,…0,4,8,16,25,35,46,58,72,88,….

把 array size 翻倍可能会浪费一些空间，但是分析起来会比较容易。

3. 分析

Indexing and assigning

The index operator and assigning to an array location are both 𝑂(1).

我们之前提到可以用 memory address calculation 来进行 indexing，cost 是 O(1).

Even languages like C hide that calculation behind a nice array index operator, so in this case the C and the Python look very much the same.

但是在 python 中，找到 object 实际的 memory location 是比较难的，所以我们可以用 list’s built-in index operator 来做 indexing，Python source code 如下：

# listobj.c
def __getitem__(self, idx):
    if idx < self.last_index:
        return self.my_array[idx]
    raise LookupError("index out of bounds")

def __setitem__(self, idx, val):
    if idx < self.last_index:
        self.my_array[idx] = val
    raise LookupError("index out of bounds")

Append

The append operation is 𝑂(1) on average, but 𝑂(𝑛) in the worst case.

只有在 last_index 是 power of 2 的时候才是 O(n)，因为需要 resize。

我们可以把这个 cost 平均到每个 append operation 里面 -> amortize/spread out the cost，数学计算如下：

For example, consider the case where you have already appended four items: each of these four appends cost you just one operation to store in the array that was already allocated to hold four items. When the fifth item is added a new array of size 8 is allocated and the four old items are copied. But now you have room in the array for four additional low cost appends.

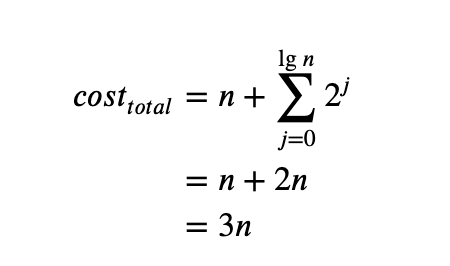
这个 cost 的范围是：0 to the base 2 log of n

• upper bound 让我们知道需要 double size 多少次
• $2^j$ 代表我们在 array double 时需要 copy 的 element
• 因为总的 cost 是 3n，所以每个 item 的 cost 就是 3n/n = 3，所以我们也可以说这是 O(1)

This kind of analysis is called amortized analysis（平摊分析） and is very useful in analyzing more advanced algorithms.

Insertion

Inserting an item into an arbitrary(random) position is 𝑂(𝑛).

这个操作中，我们需要先 shift list 里面的所有 item，给新的 item 留出位置。

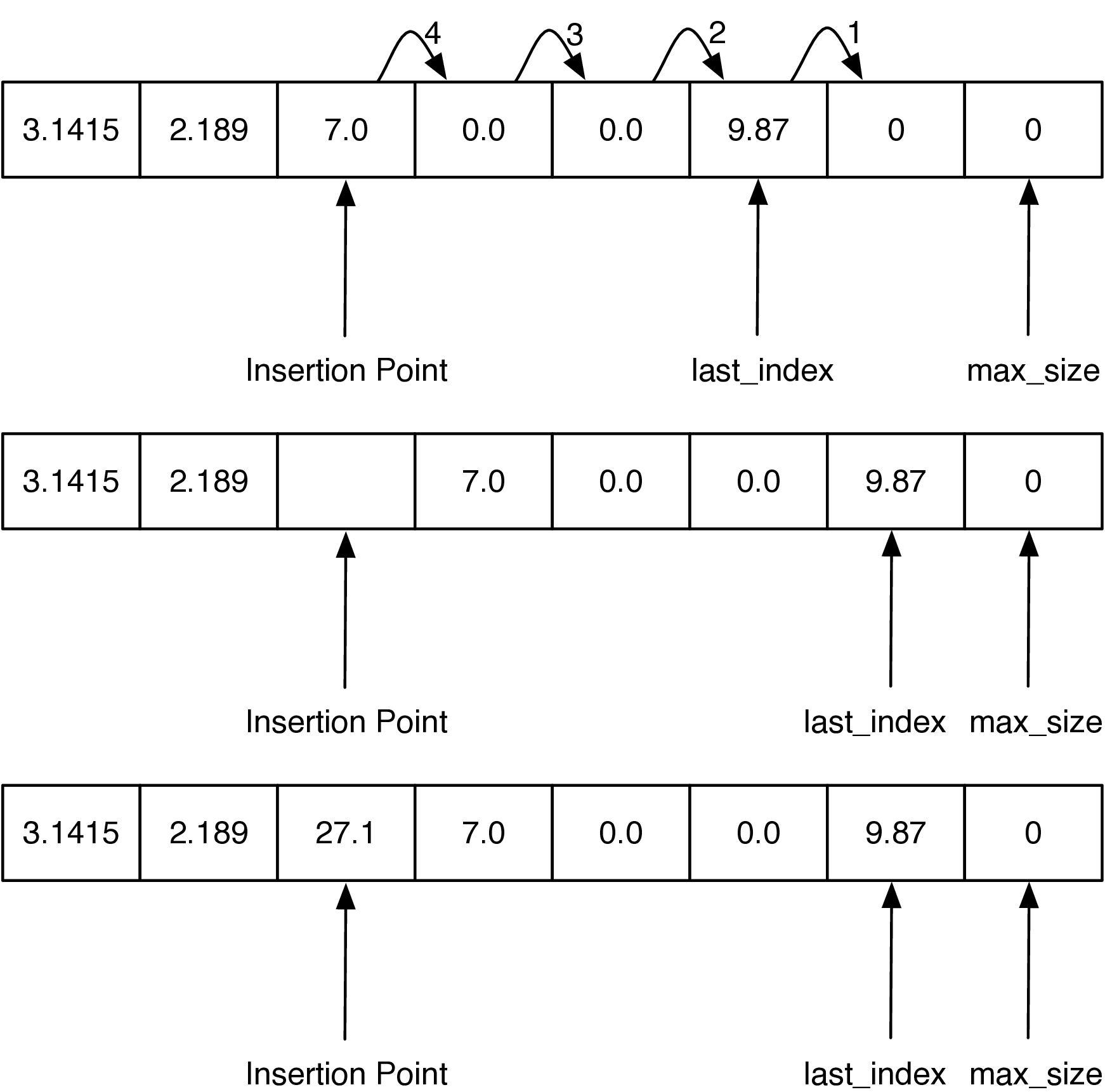
这一步的关键在于，你不希望 overwrite 任何 data，所以你需要从 list 的最后一个 element 开始，把 data copy 到一个没有 data 的位置，然后再把前一个 copy 到这个位置（应该很容易理解吧~）

def insert(self, idx, val):
    if self.last_index > self.max_size - 1:
        self.__resize()
    for i in range(self.last_index, idx - 1, -1): # range
        self.my_array[i + 1] = self.my_array[i]
    self.last_index += 1
    self.my_array[idx] = val

Note how the range is set up to ensure that we are copying existing data into the unused part of the array first, and then subsequent values are copied over old values that have already been shifted. If the loop had started at the insertion point and copied that value to the next larger index position in the array, the old value would have been lost forever.

Insertion 的复杂度是 O(n)，因为 worse case 我们要在 index = 0 的位置插入新 element，array 里面的每个 item 都要向后移动一格；

在平均情况下我们大概需要移动数量等于 array length 一半的 element，但复杂度还是 O(n) -> 可以回顾一下之前 array 的知识点。

On average we will only need to shift half of the array, but this is still 𝑂(𝑛).

我们在选择 implementation 的时候要考虑大多数的使用场景。

Neither implementation is right or wrong, they just have different performance guarantees that may be better or worse depending on the kind of application you are writing. In particular, do you intend to add items to the beginning of the list most often, or does your application add items to the end of the list? Will you be deleting items from the list, or only adding new items to the list?

Exercise

• Popping from the end of the list is 𝑂(1).

• Deleting an item from the list is 𝑂(𝑛).

There are several other interesting operations that we have not yet implemented for our ArrayList including: pop, del, index, and making the ArrayList iterable. We leave these enhancements to the ArrayList as an exercise for you.

4. 结语

Skip lists are linked lists that provide expected 𝑂(log(𝑛)) searches.