0. 前言

Reference: 9.6

文本处理是一个重要的计算机学习领域，我们经常需要从一个长的字符串里面通过一些 pattern 来匹配 substrings。

我们的任务是在搜索时返回第一个能匹配 pattern 的 substring，进阶版是匹配所有的 pattern matching substring。

find

Python 有一个 build-in substring method - find，它可以返回第一个 matching pattern 的字符串的位置。

比如下面的例子中，ab 的第一个match index=2，xyz 则没有 match，返回-1。

>>> "ccabababcab".find("ab")
2
>>> "ccabababcab".find("xyz")
-1
>>>

1. Biological Strings

算法在生物信息学领域中的应用和发展越来越受到人们的重视，比如找到一些能够 manage and process 大量生物数据的方法。

这类数据很多都是跟每个人的器官相关的，比如 DNA 数据。

DNA is basically a long sequence consisting of four chemical bases: adenine(A), thymine(T), guanine(G), and cytosine(C). These four symbols are often referred to as the “genetic alphabet” and we represent a piece of DNA as a string or sequence of these base symbols.

我们经常用ATGC这四个字母来代表DNA string，比如：ATCGTAGAGTCAGTAGAGACTADTGGTACGA。

我们的目标是从一个很长的 DNA string 中找到我们需要的 DNA string pattern。

我们要解决的问题

1. input: string of A, T, G, C
2. output: locate a particular pattern within the string

我们把 DNA string 称作 text，假如找不到 pattern 的话就返回 -1；

因为 DNA string 通常来说都是很长的，所以我们的算法需要考虑到效率。

2. Simple Comparison

思路

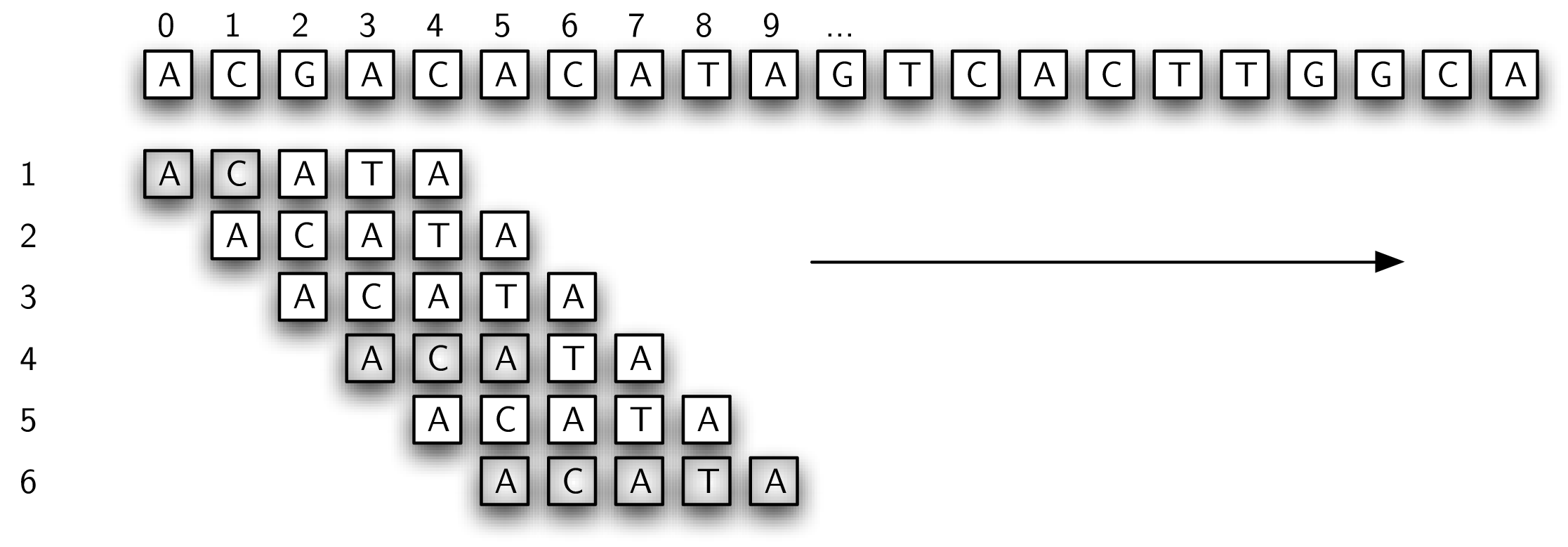
我们可以用 pattern-matching problem 来解决这个问题，我们通过尝试各种可能性来匹配 pattern（如下图）。

我们从左到右匹配，先从长 string 和 search pattern 第一个 character 开始，假如匹配成功，我们就匹配第二个 character，假如没有匹配，就把 pattern 右移一位。

在这个例子中，我们在第六次尝试中匹配到了第一个 substring，从 index 5 开始。

Code

1. It takes the pattern and the text as parameters.
2. If there’s a match, return starting text index, -1 means search failed
3. i 和 j 用来标记 text 和 pattern 的当前位置，当 text 或者 pattern 结束时跳出循环
4. 当找到一个 match，我们把 j 的数值 + 1，假如没有 match，j reset 到 0，不管找没找到 match，i 的位置都向右移动一格

def simple_matcher(pattern, text):
    i = 0
    j = 0

    while True:
        if text[i] == pattern[j]: # check match
            j = j + 1
        else:
            j = 0
        i = i + 1

        if i == len(text): # check if reach end
            return -1
        if j == len(pattern): # check if find a match
            return i - j

复杂度

假如 length of text = n, length of pattern = m, 那么时间复杂度 = O(nm)，因为每个 text 里面的字符都可能要匹配 pattern 里面的每个字符（假如找不到）。

这个时间复杂度在搜索长字符串的时候就显得不够理想了。

3. Graph: Finite State Automata

假如我们想要让 pattern-matcher 达到 O(n) 的复杂度呢？

有一种方法是创建一个 deterministic finite automaton (DFA)，中文名叫做 确定有限状态自动机 ，也被称为有限自动机/时序机，是有限离散数字系统的抽象数字模型。

没有学过高数的我看到离散数学表示有点慌。。

这个 DFA 使用 graph 来代表 pattern，每个 vertex/node 就是一个 state, keeping track of the amount of the pattern that has been seen so far.

每个 edge 代表的是 a transition that takes place after processing a character from the text.

感觉还是有点抽象，来看个图吧：

这张图是代表 ACATA 这个 pattern 的 DFA，第一个 vertex（数字0）被称为 start state/ initial state，代表我们目前没有看到任何 match character.

Final state 用两层圈圈表示（state 5），这个 state 没有任何的 out edge，就是只进不出的一个 node。

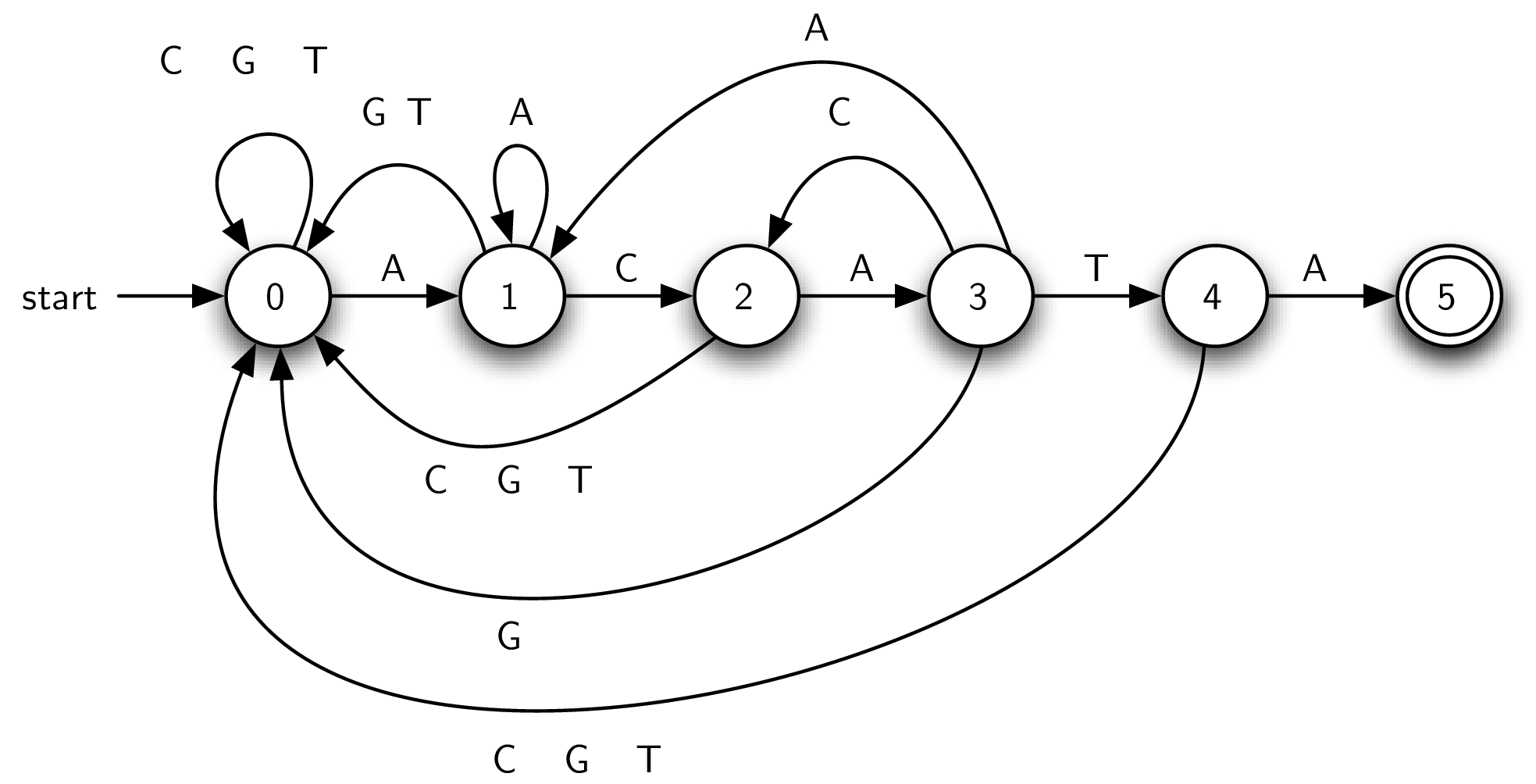
How DFA works?

首先，在开始 match 前 set to 0；

然后当我们读文本的下一个字符时，根据字符的值，我们会用一个合适的 transition (edge) 来进入下一个 state（B），state B 就成为 new current state。

根据定义，每个 state 有且仅有一个到其他 character 的 transition。所以 DNA 的 DFA 图里面，每个 state 都有 4 个到达其他 state 的 transition。

上面的示例图是简化过的，你会发现有些时候一根线上有三个字母，实际上这是三根线哦~

By definition, each state has one and only one transition for each character in the alphabet.

Note that in the figure we have labeled some edges (transitions) with multiple alphabet symbols to denote more than one transition to the same state.

我们跟着 transition 来走，直到一个结束事件发生。假如我们进入了 state 5/ final state，那么我们可以停止并且返回 success（DFA 找到了一个 pattern match），我们可以通过 current character index 和 pattern size 来找到 pattern start index。

另一方面，当我们已经找完了所有的 text character，current state 不是 final state，就说明没有 match，这个 state 被称为 “nonfinal” state。

Step by Step Table

text string: ACGACACATA

pattern: ACATA

The next state computed by the DFA always becomes the current state in the subsequent step.

每个 current state-current character 的组合都有且仅有一个。

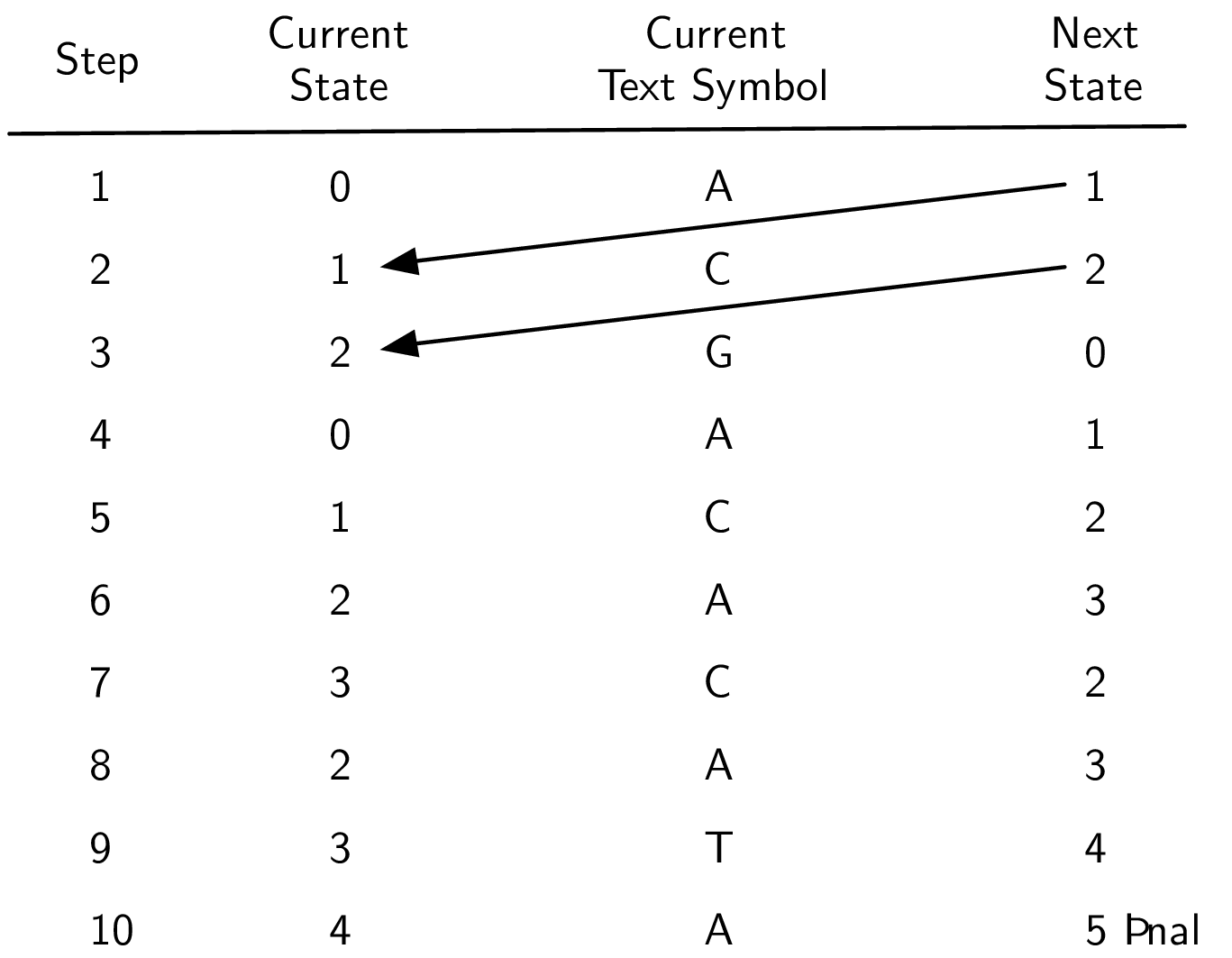
Analysis

每个 text character 都只进入一次 DFA graph，所以时间复杂度是 O(n), 但是我们还需要考虑构建 DFA 的过程（也就是准备阶段）。

有很多算法可以通过一个 pattern 来输出一个 DFA graph，不过它们都很复杂，因为每个 state 都必须有到其他 character 的 transition。

所以我们还是要继续寻找一种更高效的 pattern-matcher。

Unfortunately, all of them are quite complex mostly due to the fact that each state (vertex) must have a transition (edge) accounting for each alphabet symbol.

The question arises as to whether there might be a similar pattern-matcher that employs a more streamlined set of edges.

4. 对简单匹配的优化思考

第一种简单解法复杂度高的原因是，每次匹配失败我们都右移一格，那么是否可以多移动几格来提高效率呢？

比如下面这张图，我们在 match 失败的时候移动的格数就是不固定的。

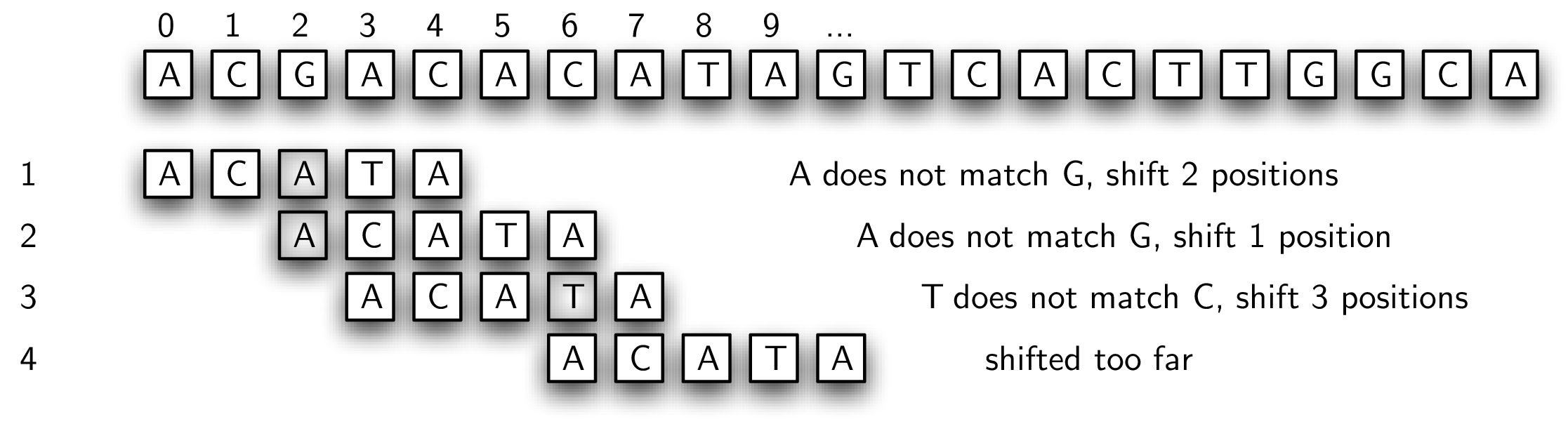
我们来看第一次，我们把 AC 匹配上了，但是第三个字母没有匹配，所以我们直接把整个 pattern 移动到没有匹配的这个字母的位置，再次开始重新匹配。

第二次匹配，0 个字符匹配，我们只能右移一格。

第三次匹配，match 了三个字符，但是第四个没有 match，所以我们移动到第四个字符的位置。

但是问题来了，我们移动的时候移过头了。。miss 掉了一个 match。

为什么会 miss？

我们没有利用 information about the content of the pattern，在第三次匹配的时候，5 号位置和 6 号位置其实是匹配 pattern 的前两个字符的。

也就是说，pattern 的前两个字符 match text string 的后面两个字符。

We say that a two-character prefix of the pattern matches a two-character suffix of the text string processed up to that point.

这是一个重要的信息，假如我们记录 pattern prefix（前缀） 和 current substring suffix（后缀）的 overlap，就可以在第三次匹配失败的时候只移动 2 个字符，第四次匹配就不会 miss 掉 match 了。

5. KMP Graph

这种 pattern-matcher 叫做 Knuth-Morris-Pratt (or KMP)，核心观点是创建一个 graph，可以提供关于 slide amount 的信息，避免 mismatch 的发生。

KMP Graph 也是包含 state 和 transition 的（跟我们之前讲的 DFA 差不多），但是每个 state 只有两个 out transition。

The KMP graph will again consist of states and transitions (vertices and edges). However, unlike the DFA graph from the previous section, there will be only two transitions leaving each state.

Example

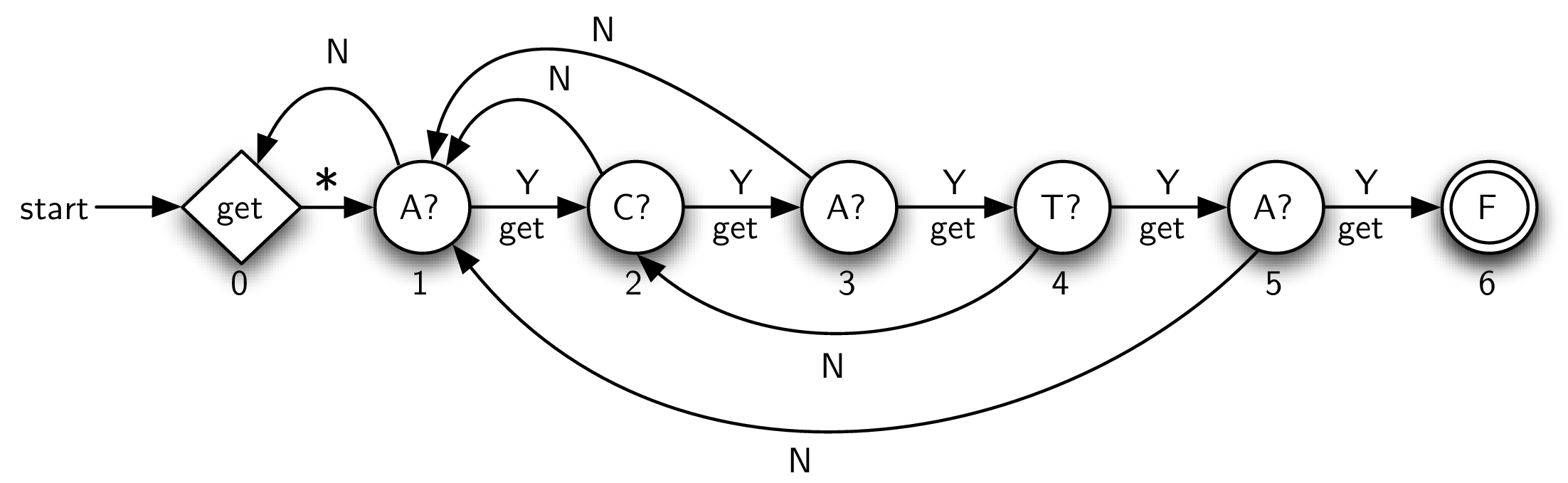
下面这张图就是一个 KMP graph 示例：

1. initial state（写着 get），用来读取 input text 的下一个字符；

2. subsequent transition（用 * 标记）是唯一的一个必经 transition。

   start 先到 initial state，get 到第一个 character，然后直接进入 state 1；

3. final state（标记为 F），同样代表 match 结束（跟 DFA 一样）；

Node Check and Labelling

每个 node 都要把当前的字符和它代表的字符进行比对，比如写着 C 的 node，就会检查当前字符是否为 C, 假如符合，就会在 transition 加上 Y 的标签，代表有一个 match character，不管这个字符是否匹配得上，我们都会读取下一个字符；

标记为 N 的 transition 就代表没有匹配，在这种情况下，我们需要知道移动多少格。

我们实际上想要保留当前的 text character，返回到这个 pattern 之前的位置。

计算这个位置，我们可以用一个简单的算法，来 check pattern against text itself，寻找 overlap between a prefix and a suffix，假如找到了 overlap，overlap length 会告诉我们应该如何移动 mismatch link。

注意：只有用了 mismatch link，才可以处理新的字符。

If such an overlap is found, its length tells us how far back to place the mismatch link in the KMP graph. It is important to note that new text characters are not processed when a mismatch link is used.

Mismatch Links Code

这个 function 返回的是一个 dictionary，包含 key value pairs，key是当前的 state，value 是 destination state for the mismatch link.

从 1 到 5 的每个 state 分别对应 pattern 里面的字符，每个 state 都可以返回到上一个 state。

mismatch link 可以通过 sliding the pattern past itself looking for the longest matching prefix and suffix 来计算。

这个 function 首先用 @ 来代表 state 0（inital state），然后加上 pattern string，构造 aug_pattern 变量。

aug_pattern 的每个字符的 index 都是对应 KMP graph 的。

然后我们创建 dict，初始化为包含从 state 1 到 state 0 的一个 key value pair，在循环中我们 check pattern 的 substring，寻找 prefix 和 suffix 的overlap。

假如找到了 overlap，就把 length of overlap 用于 set next link。

def mismatch_links(pattern):
    aug_pattern = "@" + pattern
    links = {1: 0}
    for k in range(2, len(aug_pattern)):
        s = links[k - 1]
        while s >= 1:
            if aug_pattern[s] == aug_pattern[k - 1]:
                break
            else:
                s = links[s]
        links[k] = s + 1
    return links
  
>>> mismatch_links("ACATA")
{1: 0, 2: 1, 3: 1, 4: 2, 5: 1}
>>>

KMP 分步解析

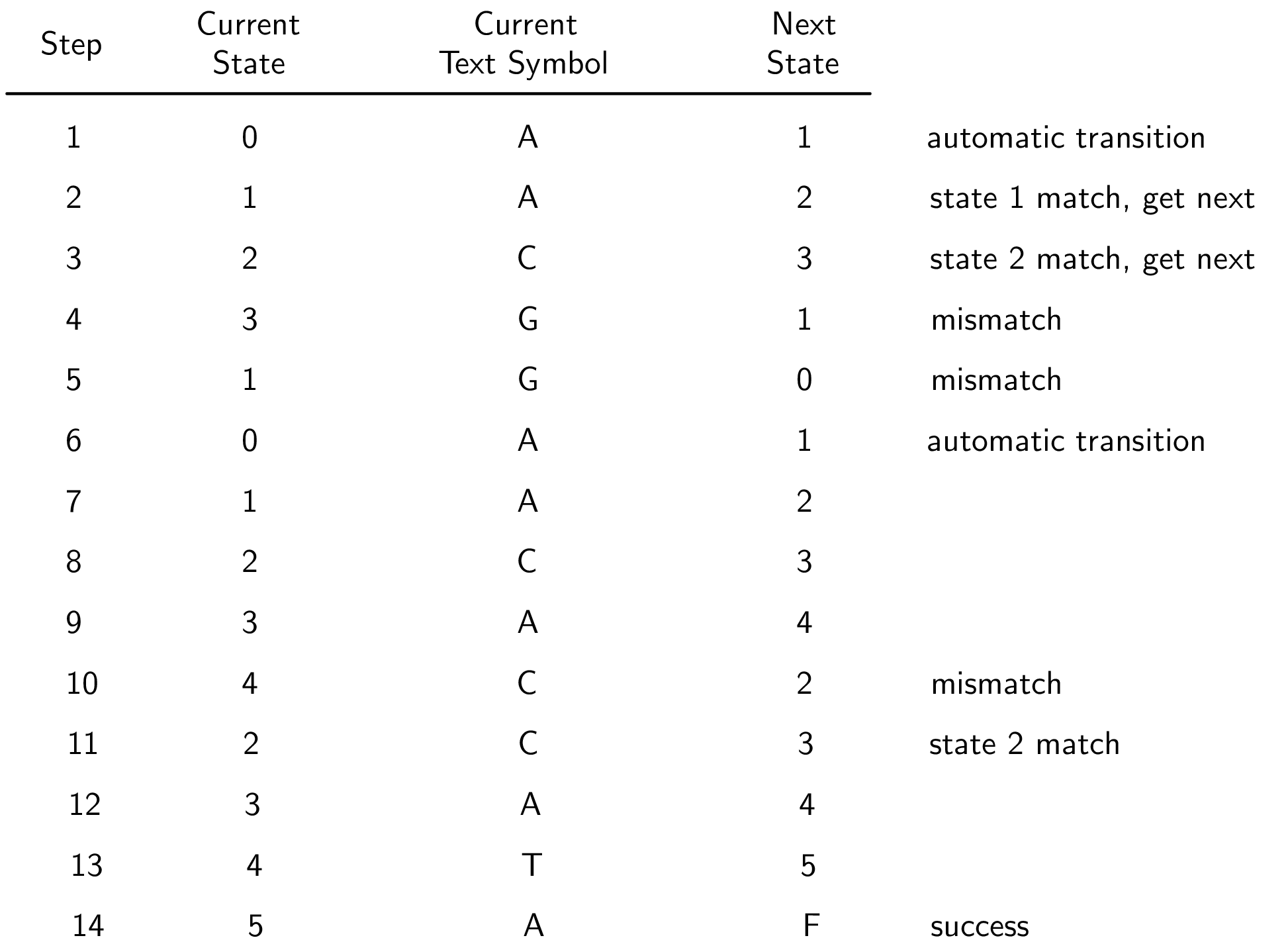
下面的例子是如何使用 KMP graph 来进行 pattern match 的分步解析。

text string = ACGACACATA

只有匹配了 match character 时，当前字符才会改变；

当 mismatch 的时候（比如第四步和第五步），当前字符不变；

到了第六步，我们回到 state 0，然后再 get next character，进入 state 1，重新开始匹配；

第十步和第十一步体现了 mismatch link 的重要性，在第十步，当前字符是 C，没有 match state 4，我们得到了一个 mismatch link；但是因为我们找到了 partial match（也就是 overlap），我们回到 state 2 而不是 state 0，因为 state 2 有 match；

我们最终找到了一个 match。

KMP Analysis

和 DFA 一样，KMP 的时间复杂度是 O(n)，因为每个字符都 process 一次。

相比于 DFA，KMP graph 构建起来要容易很多，需要的储存空间也更少，因为每个 state 只有两个 transition。

6. 结语

突然在想，Regex 是不是也用了类似的算法呀~

• Text-based pattern-matching is a very common problem in many application areas.
• Simple pattern-matching is inefficient.
• DFA graphs are easy to use but complex to build.
• KMP graphs are easy to use and easy to build.