Luna Tech

Tutorials For Dummies.

Binary Tree (1)

2021-08-08

0. 前言

Reference: 手把手带你刷二叉树（第一期） - labuladong 的算法小抄 (gitbook.io)

为什么要先刷二叉树？

因为很多经典的算法，包括回溯（Backtracking Algorithm）、动态规划（Dynamic Programming）、分治算法（Divide-and-conquer Algorithm）都是树的问题。

有人说五大常用算法是：动态规划算法，分治算法，回溯算法、贪心算法（Greedy Algorithm）以及分支限界算法（Branch and bound Algorithm）。

所有树的问题都跟树的递归遍历框架代码息息相关，二叉树相关的题目能帮助我们练好递归基本功和框架思维，而递归是学好算法的基本功，所以我们应该先刷二叉树的题目。

换言之，只要涉及递归，都可以抽象成二叉树的问题。

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    // 前序遍历（在调用所有递归function之前）
    traverse(root.left)
    // 中序遍历（在调用了一个递归function之后）
    traverse(root.right)
    // 后序遍历（在调用了所有递归function之后）
}

两种遍历框架：

相关题目

226. 翻转二叉树 - 力扣（LeetCode） (leetcode-cn.com)

114. 二叉树展开为链表 - 力扣（LeetCode） (leetcode-cn.com)

116. 填充每个节点的下一个右侧节点指针 - 力扣（LeetCode） (leetcode-cn.com)

1. 二叉树递归遍历框架的重要性

快速排序（Quicksort）和归并排序（Mergesort）这两种算法可以理解为：

为什么呢？

快速排序的代码框架

快速排序的逻辑：

注意： nums[lo...p-1] 小于等于 nums[p] 这个条件可以保证和 nums[p] 相等的元素都放在左边的 array 里面。

void sort(int[] nums, int lo, int hi) {
    /********************** 前序遍历位置 *********************/
    /* 假定我们有个 partition function，通过交换元素构建分界点 p */
    int p = partition(nums, lo, hi);
    /*******************************************************/

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

先构造分界点，然后再把问题分解成左右子数组两个小问题，分别构造子分界点，持续递归遍历。

这就是二叉树前序遍历的应用。

归并排序的代码框架

归并排序的逻辑：

void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);

    /****** 后序遍历位置 ******/
    /* 合并两个排好序的子数组  */
    merge(nums, lo, mid, hi);
    /************************/
}

先分成左右子数组，分别排序，然后合并起来，这就是分治算法。

根据 merge 的调用位置，我们可以发现这是二叉树后序遍历的应用。

2. 写递归算法的秘诀

写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要跳入递归的细节。

初学者学递归最容易犯的错误就是跳进递归里面出不来（我也是，经常把自己搞晕）。

但是我们换个思路，递归其实就是数学归纳法的应用，已知 k = 1 的时候如何，k = 2 的时候如何，k = n 的时候如何。

我们不需要再次去证明这个公式，只需要搞清楚函数的定义，并且使用这个函数就行了。

举例：计算二叉树一共有几个节点

这道题很简单，root + 左右子树的节点就是总节点数。

// 定义：count(root) 返回以 root 为根的树有多少节点
int count(TreeNode root) {
    // base case
    if (root == null) return 0;
    // 自己加上子树的节点数就是整棵树的节点数
    return 1 + count(root.left) + count(root.right);
}

那么如何计算左右子树的节点数呢？

和整棵树一样，root’ + 左右子树’ 的节点数。

这就是递归的思维了。

写树相关的算法/递归算法，简单说就是，先搞清楚当前 root 节点「该做什么」以及「什么时候做」，然后根据函数定义递归调用子节点，递归调用会让子节点做相同的事情。

3. 题目实战

226. 翻转二叉树

226. 翻转二叉树

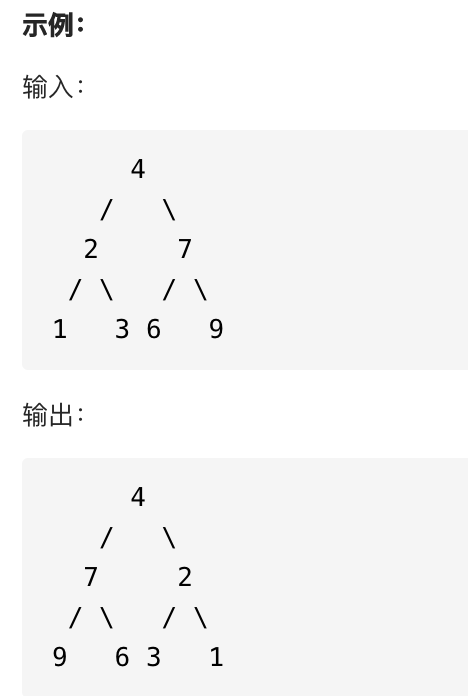
输入：二叉树节点 root

输出：镜像翻转的二叉树节点 root

思路：把每个节点的左右节点互换

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
      	// 特殊 case
        if (root == null)
            return null;
        // 前序遍历，左右互换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        // 进入递归，左右子树重复操作
        invertTree(root.left);
        invertTree(root.right);
        // 返回结果
        return root;
    }
}

其他解法

我们是否可以使用后序遍历来完成这个题目呢？

答案是：可以，前序和后序在这个题目里面不重要，只要两个 invertTree 放在一起就行了。

class Solution {
    public TreeNode invertTree(TreeNode root) {
      	// 特殊 case
        if (root == null)
            return null;
        // 进入递归，左右子树重复操作
        invertTree(root.left);
        invertTree(root.right);
        // 后序遍历，左右互换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        // 返回结果
        return root;
    }
}

我们是否可以用中序遍历来完成这个题目呢？

答案是：可以，但是得改动。

假如你按照之前的代码，只是换个位置的话，root.right 其实在进行第二次递归的时候已经变成了 root.left。

// not working
class Solution {
    public TreeNode invertTree(TreeNode root) {
      	// 特殊 case
        if (root == null)
            return null;
        // 进入递归，左子树重复操作
        invertTree(root.left);
        // 中序遍历，左右互换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        // 进入递归，右子树重复操作
        invertTree(root.right);

        // 返回结果
        return root;
    }
}

所以呢，假如你要用中序遍历，得把 invertTree(root.right); 改成 invertTree(root.left);

class Solution {
    public TreeNode invertTree(TreeNode root) {
      	// 特殊 case
        if (root == null)
            return null;
        // 进入递归，左子树重复操作
        invertTree(root.left);
        // 中序遍历，左右互换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        // 进入递归，右子树重复操作
        invertTree(root.left); // 注意这里的 node 实际上是之前的 right
        // 返回结果
        return root;
    }
}

116. 填充每个节点的下一个右侧节点指针

116. 填充每个节点的下一个右侧节点指针

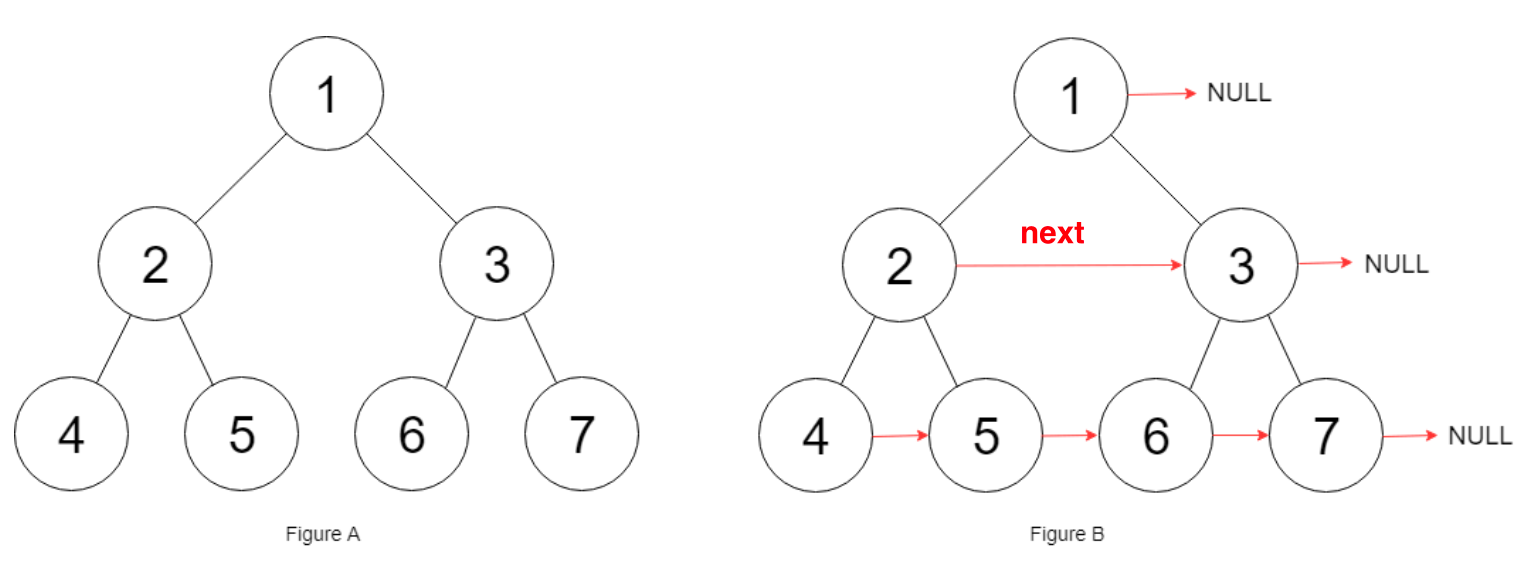
这道题目要求我们把每一层的左右节点联系起来。

root.left.next = root.right; 就是我们的核心逻辑；

那我们想到的第一个解法可能是这样的：

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if (root == null || root.left == null) {
        		return root;
    		}
        root.left.next = root.right;
        connect(root.left);
        connect(root.right);
        return root;
    }
}

但是这个解法有问题，什么问题呢？

我们没法把 5 和 6 连起来啊！因为它俩不属于一个子树。

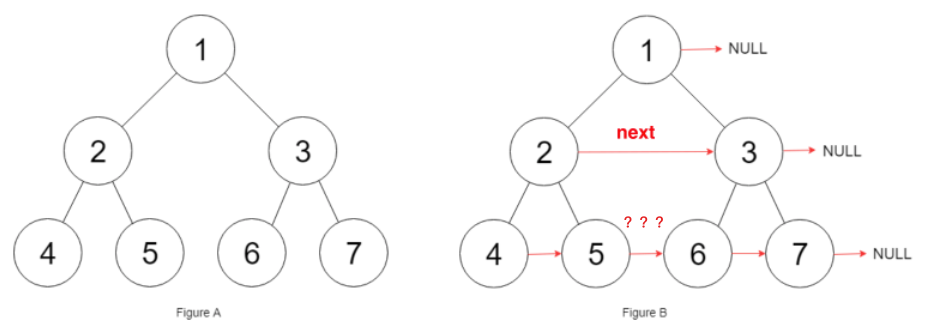
那怎么办呢？

我们要利用节点 2 和 3 之间的关系，已知 root.left.next = root.right;，那么 root.left.right.next = root.left.next.left; 就可以建立两个子树之间的关系了。

但是我们要怎么用递归的方式来抽象出这个逻辑呢？

我们可以通过写一个辅助 function，输入两个节点（左右子树 root），然后把这两个节点的子树 node 之间建立联系，也就是把「每一层二叉树节点连接起来」这个问题抽象成「将每两个相邻节点都连接起来」：

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    // 主函数
    public Node connect(Node root) {
        if (root == null) return null;
        connectTwoNode(root.left, root.right);
        return root;
    }

    // 辅助函数
    void connectTwoNode(Node node1, Node node2) {
        if (node1 == null || node2 == null) {
            return;
        }
        /**** 前序遍历位置 ****/
        // 将传入的两个节点连接
        node1.next = node2;

        // 连接相同父节点的两个子节点
        connectTwoNode(node1.left, node1.right);
        connectTwoNode(node2.left, node2.right);
        // 连接跨越父节点的两个子节点
        connectTwoNode(node1.right, node2.left);
    }
}

这样，connectTwoNode 函数不断递归，把两个子树的内部节点联系起来的同时，也把两个子树之间的节点连起来，就可以解决问题了。

114. 二叉树展开为链表

114. 二叉树展开为链表

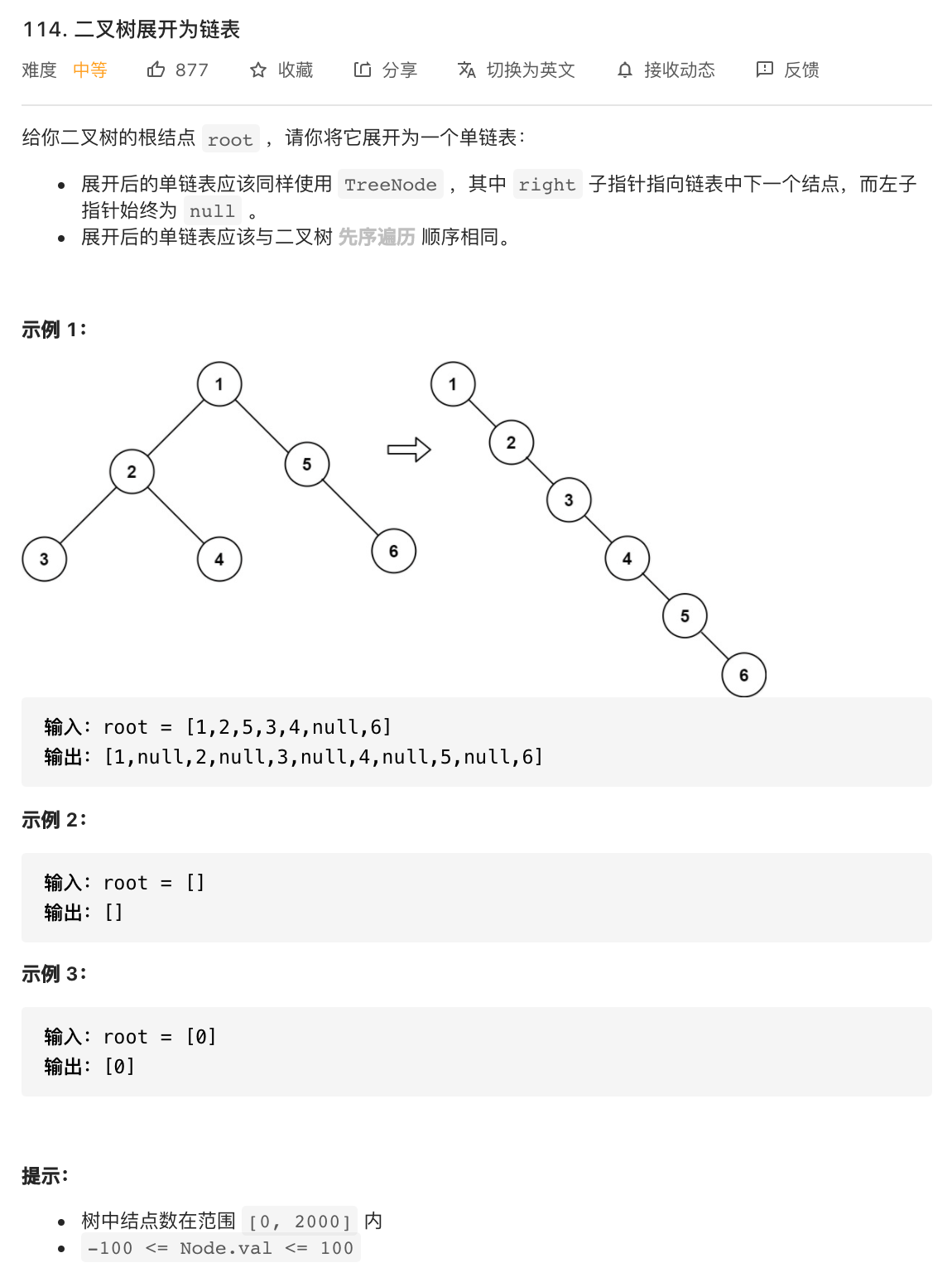
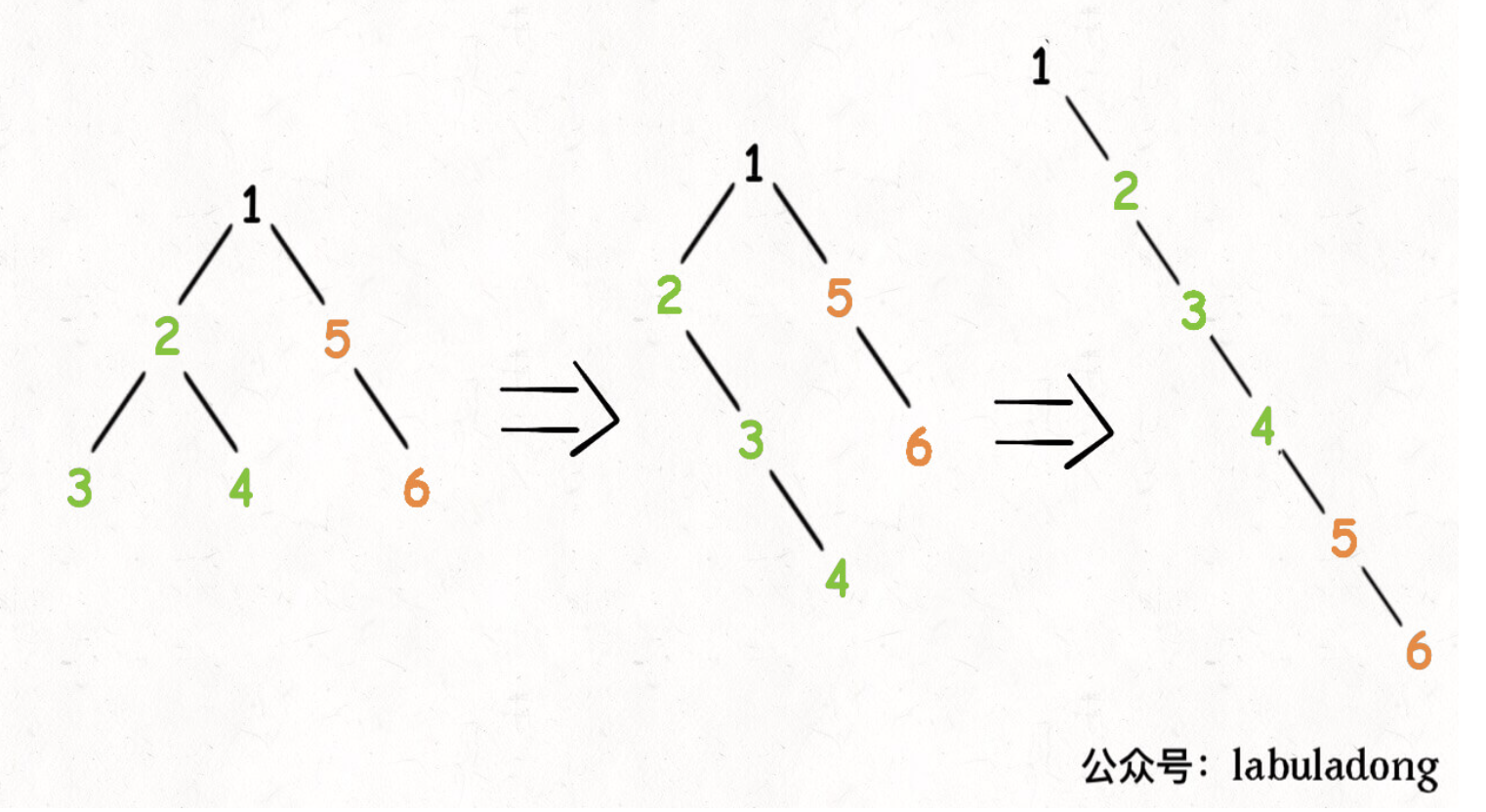
Ref: labuladong

思路：从最小 case 开始考虑，当 root 只有一个左节点和一个右节点的时候，我们需要把左节点变成右节点，再把原右节点变成新右节点的右节点。

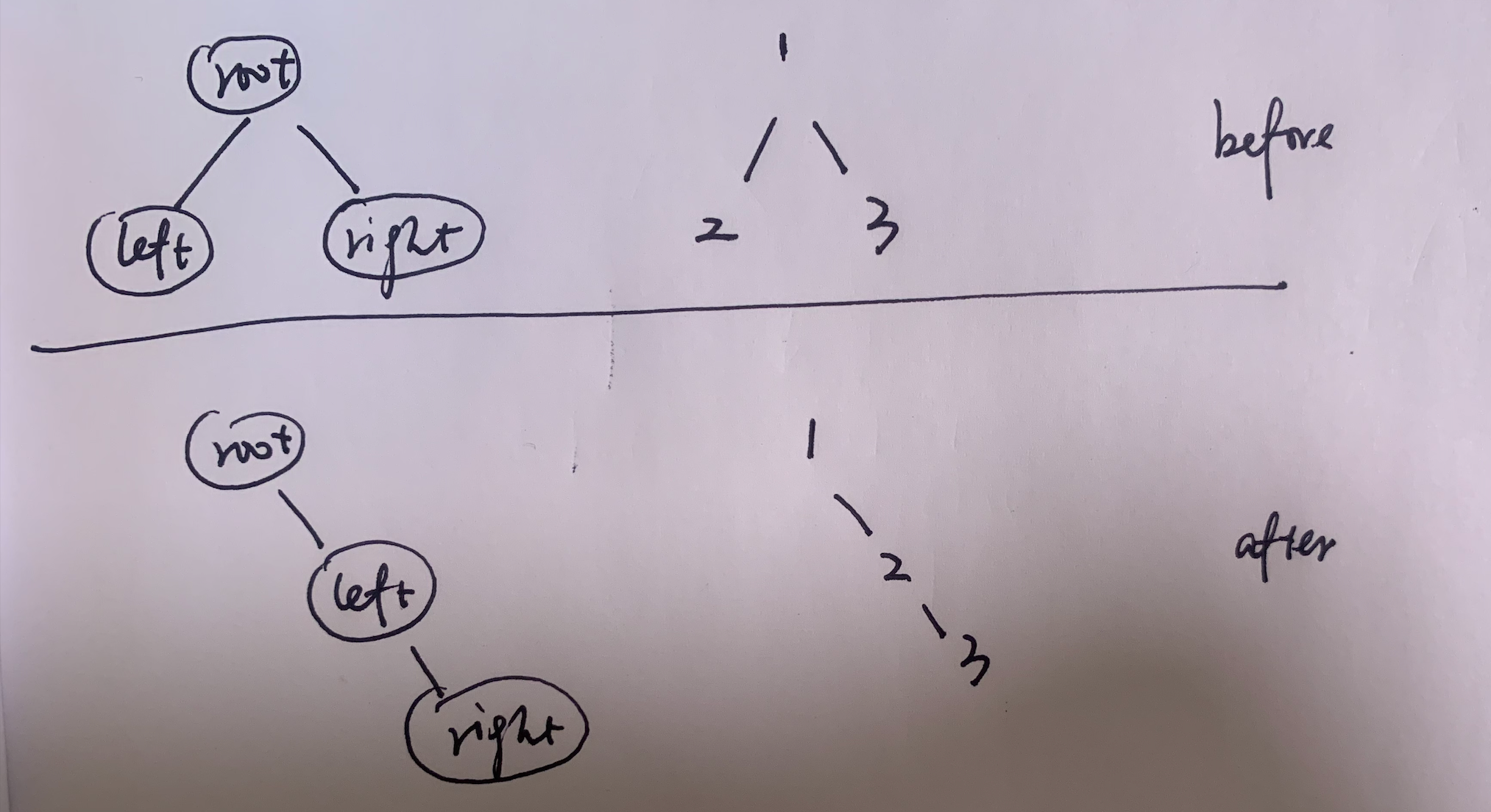
这段代码可以表示为：

TreeNode orgRight = root.right;
root.right = null;
root.right = root.left;
root.right.right = orgRight;

那么，假设 root.left 和 root.right 都是经过 flatten 之后的结果，我们只需要最后返回 root 即可。

PS: 题目给的 method 是 void type，所以我们不需要 return root，只需要 return 就可以了（有点绕）。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 定义：将以 root 为根的树拉平为链表
    public void flatten(TreeNode root) {
        // base case, 根据题目示例2来写
        if (root == null) return;
				// flatten both left and right trees
        flatten(root.left);
        flatten(root.right);

        /**** 后序遍历位置 ****/
        // 1、左右子树已经被拉平成一条链表
        TreeNode left = root.left;
        TreeNode right = root.right;

        // 2、将左子树作为右子树
        root.left = null;
        root.right = left;

        // 3、将原先的右子树接到当前右子树的末端
        TreeNode p = root;
        while (p.right != null) {
            p = p.right;
        }
        p.right = right;
    }
}

为什么要做后序遍历呢？

因为我们的假设是 root.left 和 root.right 都已经经过 flatten 了，所以我们只需要关注如何把最小 case 的节点进行 flatten 即可。

假如我们要做前序遍历的话，调用 flatten 递归的时候 root.left 和 root.right 需要指向最初的那两个 node。

class Solution {
    public void flatten(TreeNode root) {
        // base case
        if (root == null) return;

        /**** 前序遍历 ****/
        // 1、储存最初的左右节点
        TreeNode left = root.left;
        TreeNode right = root.right;

        // 2、进行第一步 flatten 操作（左子树）
        root.left = null;
        root.right = left;

        // 3、进行第二步 flatten 操作（右子树）
        TreeNode p = root;
        while (p.right != null) {
            p = p.right;
        }
        p.right = right;

        // 调用递归（使用未经改变的两个节点）
        flatten(left);
        flatten(right);
    }
}