Luna Tech

Tutorials For Dummies.

Binary Tree (2)

2021-08-18

0. 前言

Reference: 东哥手把手帮你刷通二叉树|第二期 (qq.com)

树的算法的关键思路

把题目的要求细化，搞清楚根节点应该做什么，然后剩下的事情抛给前/中/后序的遍历框架就行了。

相关题目

654. 最大二叉树 - 力扣（LeetCode） (leetcode-cn.com)

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode） (leetcode-cn.com)

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode） (leetcode-cn.com)

1. 654 - 构造最大二叉树

654. 最大二叉树 - 力扣（LeetCode） (leetcode-cn.com)

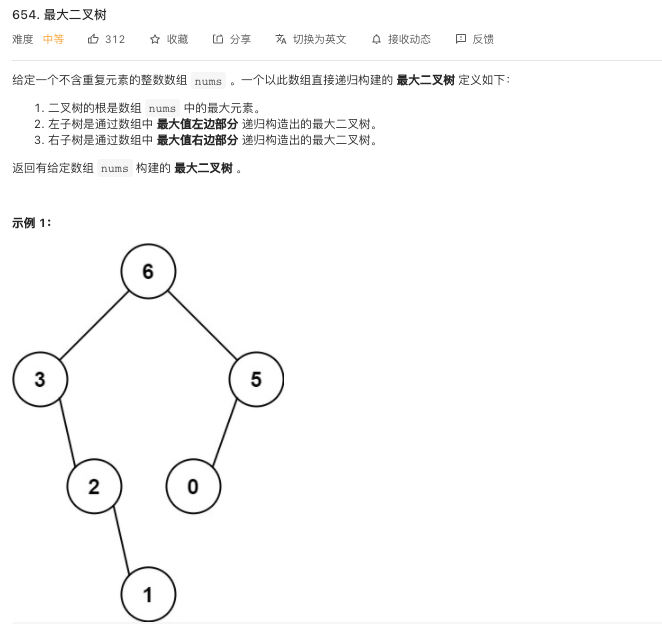
分析

输入：一个整数数组

输出：一个最大二叉树的根节点

思路：遍历数组找到最大值，然后在最大值的左边数组和右边数组重复调用找到最大值的 function（递归）

Step 1：把题目中的信息代入到 function 里面

TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
    // 找到数组中的最大值
    TreeNode root = new TreeNode(6);
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

Step 2：写伪代码（pseudocode）

这里的关键是 maxVal 和 maxValIndex 这两个变量，它能够记录我们当前遍历的数组的最大值以及位置。

注意初始值要设为 int.min 和 -1。

TreeNode constructMaximumBinaryTree(int[] nums) {
    if (nums is empty) return null;
    // 找到数组中的最大值
    int maxVal = Integer.MIN_VALUE-1;
    int maxValIndex  = -1;
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] > maxVal) {
            maxVal = nums[i];
            maxValIndex  = i;
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree(nums[0..maxValIndex -1]);
    root.right = constructMaximumBinaryTree(nums[maxValIndex+1..nums.length-1]);
    return root;
}

Step 3：做题

  1. 我们用了一个辅助 function 来构造最大二叉树；
  2. low 和 high 分别对应当前数组的 min-index 和 max-index；
  3. 当 min-index > max-index 的时候跳出递归
    1. 当 build(nums, low, maxValIndex - 1) 里面 low = 0, maxValIndex = 0 的时候，跳出递归
    2. 当 build(nums, maxValIndex + 1, high) 里面 maxValIndex == high 的时候，maxValIndex + 1 > high，跳出递归
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
				return build(nums, 0, nums.length - 1);
    }

    /* 将 nums[low..high] 构造成符合条件的树，返回根节点 */
    TreeNode build(int[] nums, int low, int high) {
        // base case - 当数组只有一个元素时结束递归
        if (low > high) {
            return null;
        }

        // 找到数组中的最大值和对应的索引
        int maxValIndex = -1, maxVal = Integer.MIN_VALUE;
        for (int i = low; i <= high; i++) {
            if (maxVal < nums[i]) {
                maxValIndex = i;
                maxVal = nums[i];
            }
        }

        TreeNode root = new TreeNode(maxVal);
        // 递归调用构造左右子树
        root.left = build(nums, low, maxValIndex - 1);
        root.right = build(nums, maxValIndex + 1, high);

        return root;
    }
}

2. 105 - 从前序与中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode） (leetcode-cn.com)

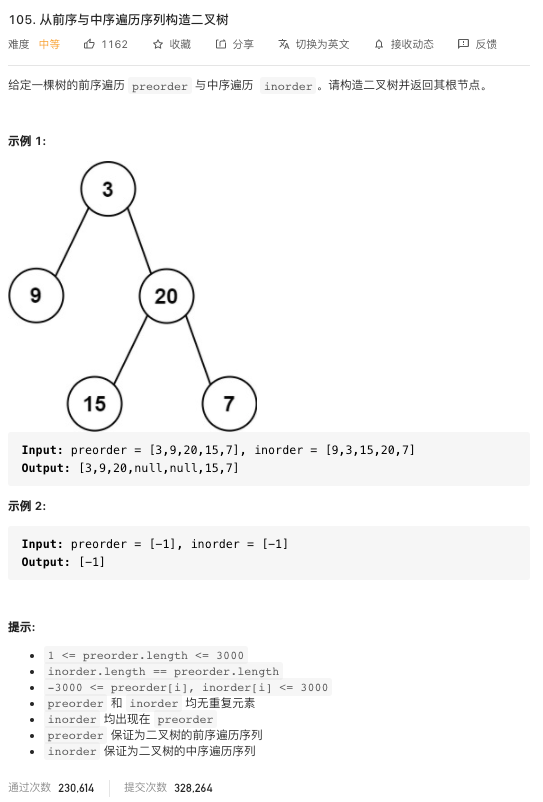
分析

输入：一个 preorder 数组，一个 inorder 数组

输出：二叉树的根节点

思路：确定根节点的值，然后构造左右子树（递归）

难点：如何确定左右子树的起始和结束位置

复习：前序遍历和中序遍历

void traverse(TreeNode root) {
    // 前序遍历
    preorder.add(root.val);
    traverse(root.left);
    traverse(root.right);
}

void traverse(TreeNode root) {
    traverse(root.left);
    // 中序遍历
    inorder.add(root.val);
    traverse(root.right);
}

前序遍历很好理解，就是先 root，左边子树遍历完了再遍历右边子树。

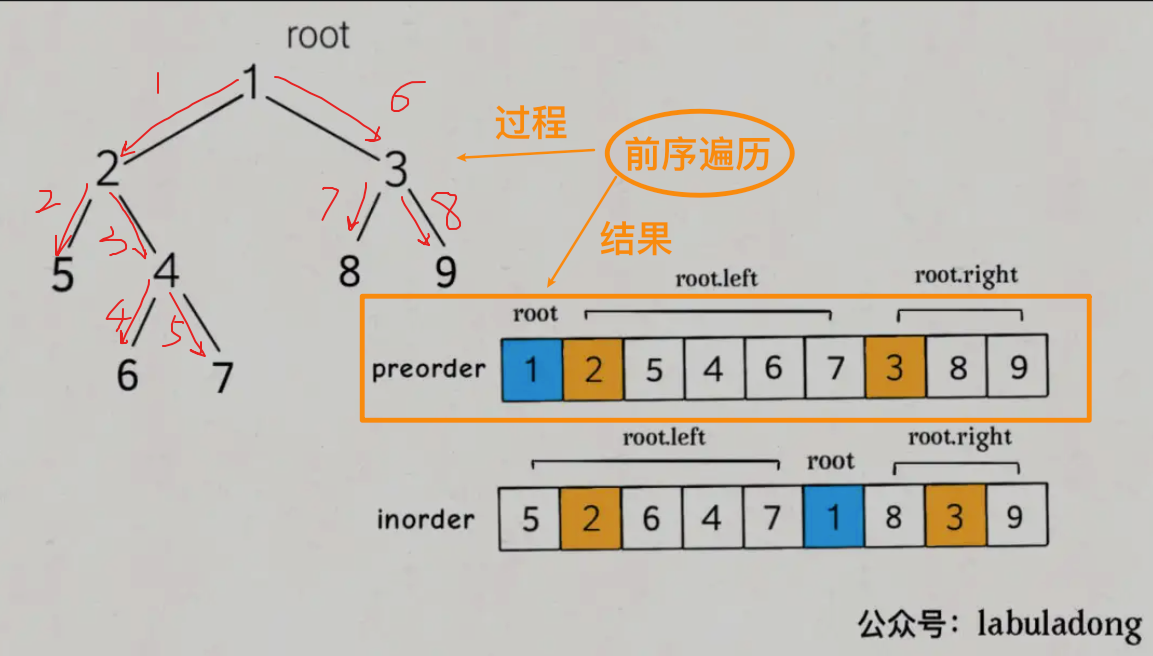
中序遍历有点绕，起始点是左边子树的最左 node，左边子树的最右 node 会指向 root，然后再遍历右边子树，先从最左开始，到最右结束。

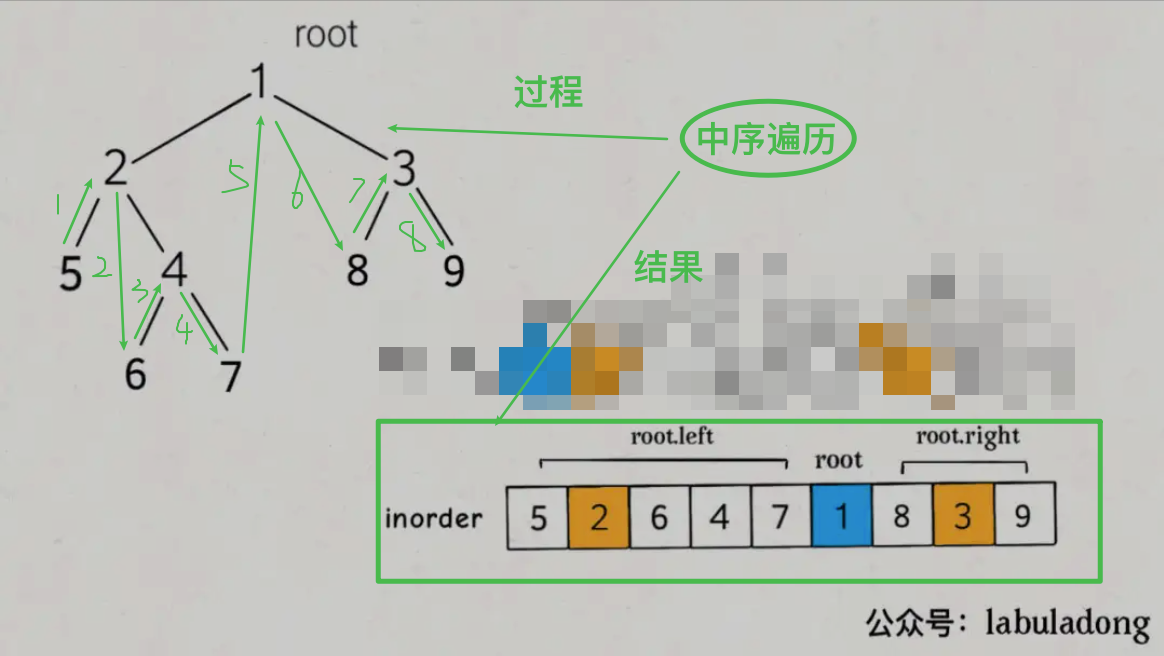
怎么找到根节点

但是我们怎么确定 preorder 和 inorder 里面左右子树的分割点呢？

也就是说，下面这段代码中，我们要想办法填上 ? 部分的值。

/* 主函数 */
TreeNode buildTree(int[] preorder, int[] inorder) {
    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
}

/* 
   若前序遍历数组为 preorder[preStart..preEnd]，
   后续遍历数组为 postorder[postStart..postEnd]，
   构造二叉树，返回该二叉树的根节点 
*/
TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {
    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int inRoot = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            inRoot = i;
            break;
        }
    }

    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, ?, ?,
                      inorder, ?, ?);

    root.right = build(preorder, ?, ?,
                       inorder, ?, ?);
    return root;
}

Step 1：已知 preorder 和 inorder 里面的 rootIndex

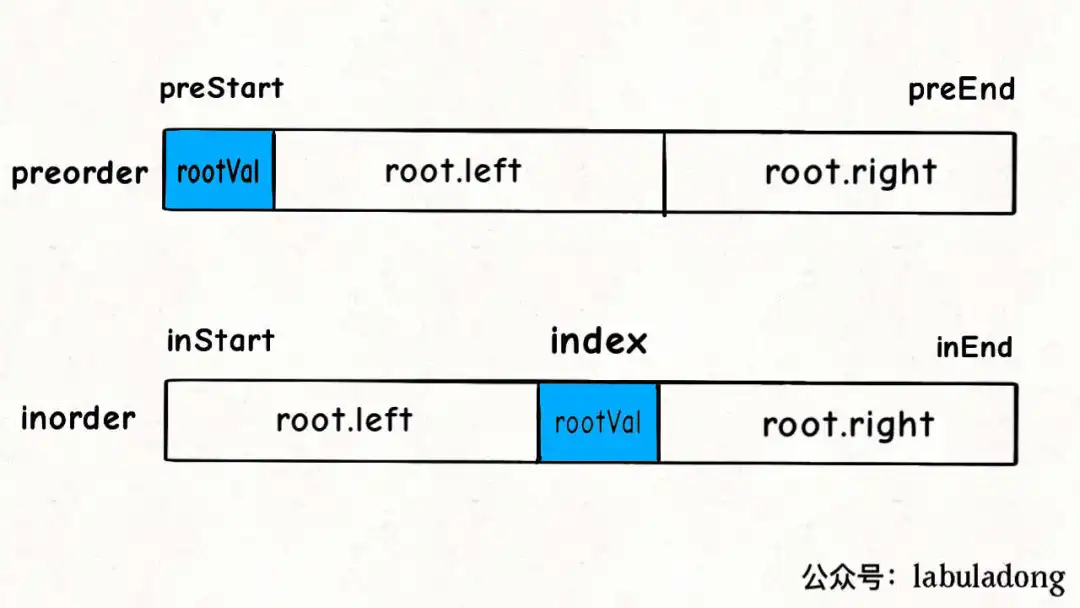
Step 2：确定 inorder 的左右子树 start-index 和 end-index

根据 inorder 的特性，我们知道起始部分是左子树，root 之后是右子树。

root.left = build(preorder, ?, ?,
                  inorder, inStart, inRoot - 1);

root.right = build(preorder, ?, ?,
                   inorder, inRoot + 1, inEnd);

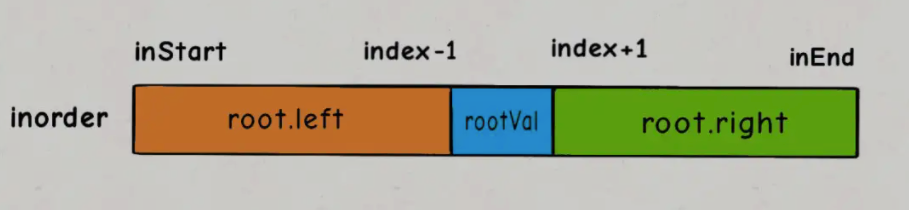
Step 3：根据 inorder 左子树的 node 数量，来划分 preorder 左右子树的分界点

int leftSize = inRoot - inStart;

root.left = build(preorder, preStart + 1, preStart + leftSize,
                  inorder, inStart, inRoot - 1);

root.right = build(preorder, preStart + leftSize + 1, preEnd,
                   inorder, inRoot + 1, inEnd);

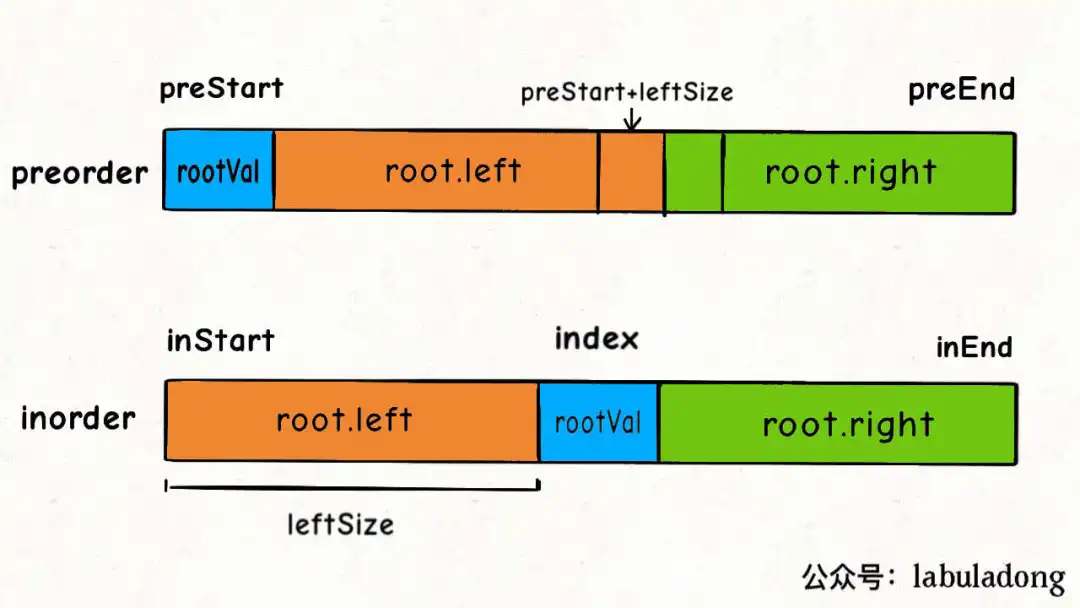
完整代码

  1. Base case 跟上一题类似，就是 start-index > end-index 的时候；
  2. 根据 left-tree-size 来计算递归 function 传入的值；
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, 0, preorder.length - 1,
                     inorder, 0, inorder.length - 1);
    }

    TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {

        if (preStart > preEnd) {
            return null;
        }

        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // rootVal 在中序遍历数组中的索引（为了计算左子树的 node size）
        int inRoot = 0;
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == rootVal) {
                inRoot = i;
                break;
            }
        }

        int leftSize = inRoot - inStart;

        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                        inorder, inStart, inRoot - 1);

        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                        inorder, inRoot + 1, inEnd);
        return root;
    }
}

3. 106 - 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode） (leetcode-cn.com)

分析

输入：一个 inorder 数组，一个 postorder 数组

输出：二叉树的根节点

思路：确定根节点的值，然后构造左右子树（递归）

难点：如何确定左右子树的起始和结束位置

复习：中序遍历和后序遍历

void traverse(TreeNode root) {
    traverse(root.left);
    // 中序遍历
    inorder.add(root.val);
    traverse(root.right);
}

void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
    // 后序遍历
    postorder.add(root.val);
}

我们发现，后序遍历和中序遍历的起点一样，都是左子树的最左 node，区别在于后序遍历在遍历完左子树之后没有回到 root，而是指向了右子树的最左 node。

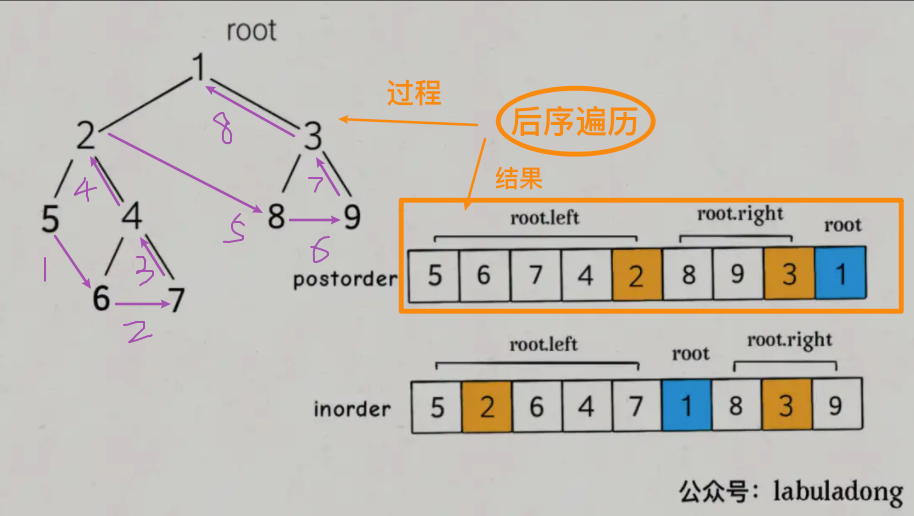
怎么找到根节点

如何确定 postorder 和 inorder 里面左右子树的分割点？和上面一样。

核心在于把下面这段代码中的 ? 填上。

TreeNode buildTree(int[] inorder, int[] postorder) {
    return build(inorder, 0, inorder.length - 1,
                 postorder, 0, postorder.length - 1);
}

TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int inRoot = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            inRoot = i;
            break;
        }
    }

    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(postorder, ?, ?,
                      inorder, ?, ?);

    root.right = build(postorder, ?, ?,
                       inorder, ?, ?);
    return root;
}

Step 1：已知 postorder 和 inorder 里面的 rootIndex

Postorder 的 root 是最后一个 index。

Step 2：确定 inorder 的左右子树 start-index 和 end-index（和上一题一样）

根据 inorder 的特性，我们知道起始部分是左子树，root 之后是右子树。

root.left = build(postorder, ?, ?,
                  inorder, inStart, inRoot - 1);

root.right = build(postorder, ?, ?,
                   inorder, inRoot + 1, inEnd);

Step 3：根据 inorder 左子树的 node 数量，来划分 postorder 左右子树的分界点

int leftSize = inRoot - inStart;

root.left = build(inorder, inStart, inRoot - 1,
                  postorder, postStart, postStart + leftSize - 1);

root.right = build(inorder, inRoot + 1, inEnd,
                   postorder, postStart + leftSize, postEnd - 1);

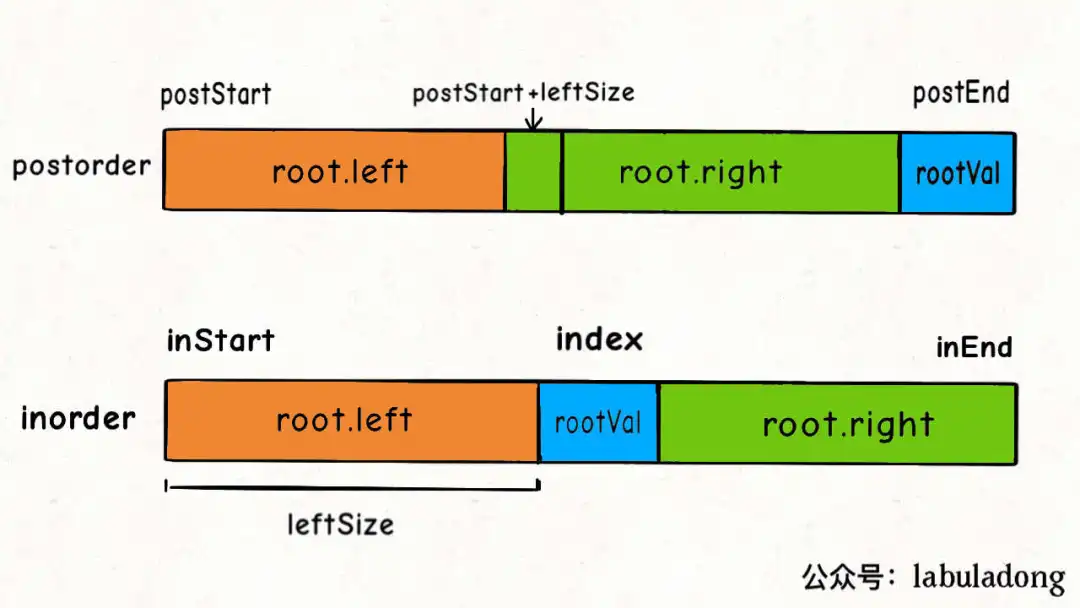
完整代码

  1. Base case 跟上一题类似，就是 start-index > end-index 的时候；
  2. 根据 left-tree-size 来计算递归 function 传入的值；
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return build(inorder, 0, inorder.length - 1,
                 postorder, 0, postorder.length - 1);
    }
  
    TreeNode build(int[] inorder, int inStart, int inEnd,
                    int[] postorder, int postStart, int postEnd) {

        if (postStart > postEnd) {
            return null;
        }

        // root 节点对应的值就是后序遍历数组的最后一个元素
        int rootVal = postorder[postEnd];
        // rootVal 在中序遍历数组中的索引（为了计算左子树的 node size）
        int inRoot = 0;
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == rootVal) {
                inRoot = i;
                break;
            }
        }

        int leftSize = inRoot - inStart;

        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(inorder, inStart, inRoot - 1,
                        postorder, postStart, postStart + leftSize - 1);

        root.right = build(inorder, inRoot + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
        return root;
    }
}

优化版本

图解构造二叉树之中序+后序 - 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode） (leetcode-cn.com)

在 Leetcode 里面发现了这个解法，有几点可以借鉴的：

  1. 加一个 inorderArrayMap，避免多次遍历 inorder 来找 root index；
  2. 不传入 postorder 和 inorder，把 postorder 存为一个 class variable；
class Solution {
    // 两个 class variable
    HashMap<Integer,Integer> inorderArrayMap = new HashMap<>();
    int[] post;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        // 将节点值及索引全部记录在哈希表中，我们就不需要每次都遍历寻找 inorder 里面 root 的 index 了
        for(int i = 0;i < inorder.length; i++) {
            inorderArrayMap.put(inorder[i], i);
        }
          
        post = postorder;
        TreeNode root = buildTree(0, inorder.length - 1, 0, post.length - 1);
        return root;
    }

    public TreeNode buildTree(int inStart, int inEnd, int postStart, int postEnd) {
        if(inEnd < inStart || postEnd < postStart) return null;

        int rootVal = post[postEnd];
        int inRoot = inorderArrayMap.get(rootVal);//获取对应的索引
        int leftSize = inRoot - inStart;

        TreeNode root = new TreeNode(rootVal);
        root.left = buildTree(inStart, inRoot - 1, postStart, postStart + leftSize - 1);
        root.right = buildTree(inRoot + 1, inEnd, postStart + leftSize, postEnd - 1);
        return root;
    }
}