Graph: General Depth First Search
2021-05-05
0. 前言
上一篇的 DFS 是一种特殊的 DFS,因为它的目标是找到一条路径,这条路径不包含任何的重复访问(也就是 create the deepest depth tree without any branches)。
1. General Depth First Search
General DFS 难还是特殊 DFS 难?
General 的 DFS 比特殊的 DFS 要容易一些,因为它的目标是尽可能深入地找、尽可能连接更多的node,需要的时候就分叉:
- search as deeply as possible,
- connecting as many nodes in the graph as possible and
- branching where necessary.
只能找到一条路径吗?
这种 DFS 可以找到不止一条路径,假如它找到了多于一条的路径,那么我们就把这些路径叫做 depth first forest(深度优先森林 - 好文艺的名字)。
如何构造 search tree?
DFS 和 BFS 一样,也会利用 predecessor 的信息来构造 tree。
DFS 的 Node 还需要额外的两个变量,一个是 discovery time,一个是 finish time。
Discovery time 用来记录这个 node 第一次被访问时我们一共走了多少步。
Finish time 就是一个 node 被标记为黑色(访问结束)之前我们一共走了多少步。
2. General DFS Code
-
Inherit from Graph class
-
dfs method 会遍历所有的 node,当一个 node 是白色(未被访问过)时,call dfsvisit method。
这么做(遍历而不是直接从 start node 开始 search)的原因是:我们要确保所有 graph 里面的 node 都查看过了,在构造 depth first forest 时不遗漏任何一条路径。
-
dfsvisit 会 explore 所有白色的neighbour node,做深度搜索。
这个 method 跟 bfs 基本是一样的,唯一的区别就是 for loop 里面最后一行的 recursive
self.dfsvisit(nextVertex)bfs 在这里是把 node 加入到了 queue 里面,稍后再搜索。
所以 bfs 用的是 queue,dfs 用的是 stack (recursive call)
# pip3 install pythonds
from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__() # inherit from Graph
self.time = 0 # extra field
# extra method
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
# extra method, helper
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)
3. 图解 DFS 步骤
1. 构造 DFS tree,从 A 开始,A 变灰色
A 的 Discovery time = 1
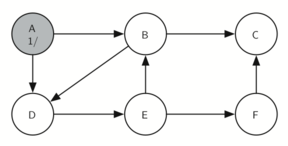
2. A 到 B
A 有两个 child,B 和 D,我们根据字母顺序选 - B
B 的 Discovery time = 2
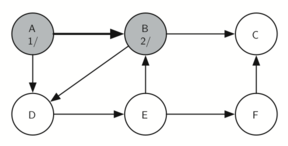
3. B 到 C (继续深入)
B 有两个 child,C 和 D,我们根据字母顺序选 - C
C 的 Discovery time = 3
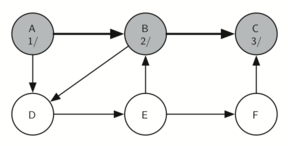
4. C 没有 child,所以变成黑色(访问结束)
C 是这个 branch 里面的最后一个 node,所以C 的 finish time = 4(注意这里即使没有访问新的 node,也要在 Discovery time 上 + 1)。
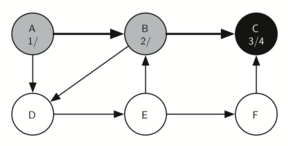
5. 回到 B,访问它的另一个 child - D
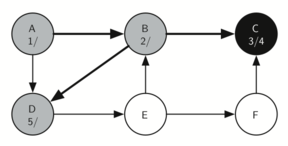
6. 继续访问 D 的 child - E
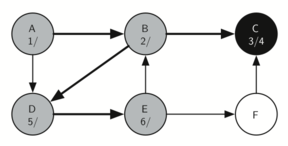
7. 继续访问 E 的 child - F
E 有两个 child - B 和 F,因为 B 已经是灰色了,所以我们不能继续访问 B(会陷入死循环)。
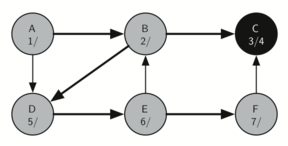
8. F 的 child 是 C,C 是黑色,所以 F 开始返回起点
F 也被标记成黑色,这个 branch 访问结束。
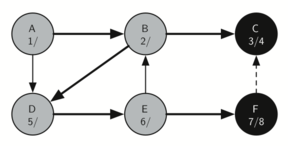
9. 从 F 返回 E,E 的两个 child 都被访问过,所以 E 变黑
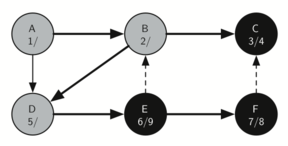
10. 从 E 返回 D,D 变黑
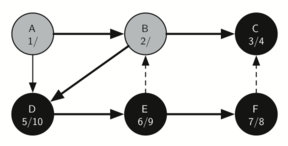
11. 从 D 返回 B,B 变黑
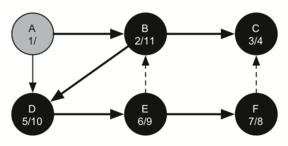
12. 从 B 回到 A,整条路径完成
A - B - D - E - F - C
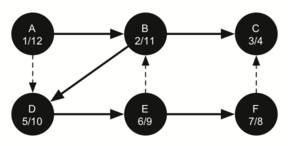
parenthesis property 括号属性
每个 node 的 discovery time 和 finish time 被称为括号属性。
它表示在 DFS tree 里面的任何一个 node 的所有 children 都有:
- 比 parent 长的 discovery time
- 比 parent 短的 finish time
The starting and finishing times for each node display a property called the parenthesis property. This property means that all the children of a particular node in the depth first tree have a later discovery time and an earlier finish time than their parent.
Breadth First Forest
我们也可以创建一个 breadth first forest,代表所有graph中两个node的最短距离。
Although our implementation of
bfswas only interested in considering nodes for which there was a path leading back to the start, it is possible to create a breadth first forest that represents the shortest path between all pairs of nodes in the graph.
4. DFS 效率分析
Main Method
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
时间复杂度: O(n)
Helper Method
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)
helper method 的时间复杂度等于一个 node 的 edge 数量,就是 O(m)。
DFS
总的时间复杂度=O(n+m)
5. 结语
这篇感觉教程只写了一半?引入了 start time 和 finish time,却没有用到这两个变量……
逻辑很清楚,图解也看懂了,但是实际的使用可能还要再查一下其他的资料。
下一篇讲的就是实际的应用 - Topological Sorting。