0. 前言

Reference: 9.3

Dictionary 有时候也被称作 Map，存的是 key-value pairs。

• key 必须 unique，用 key 可以找到对应的 value

• 所有的 dictionary 都必须提供 key-value pair 的增改查删功能以及根据 key 找 value 的功能

  比如下图中给到了key 93，我们就需要输出这个 key 对应的 value ->be

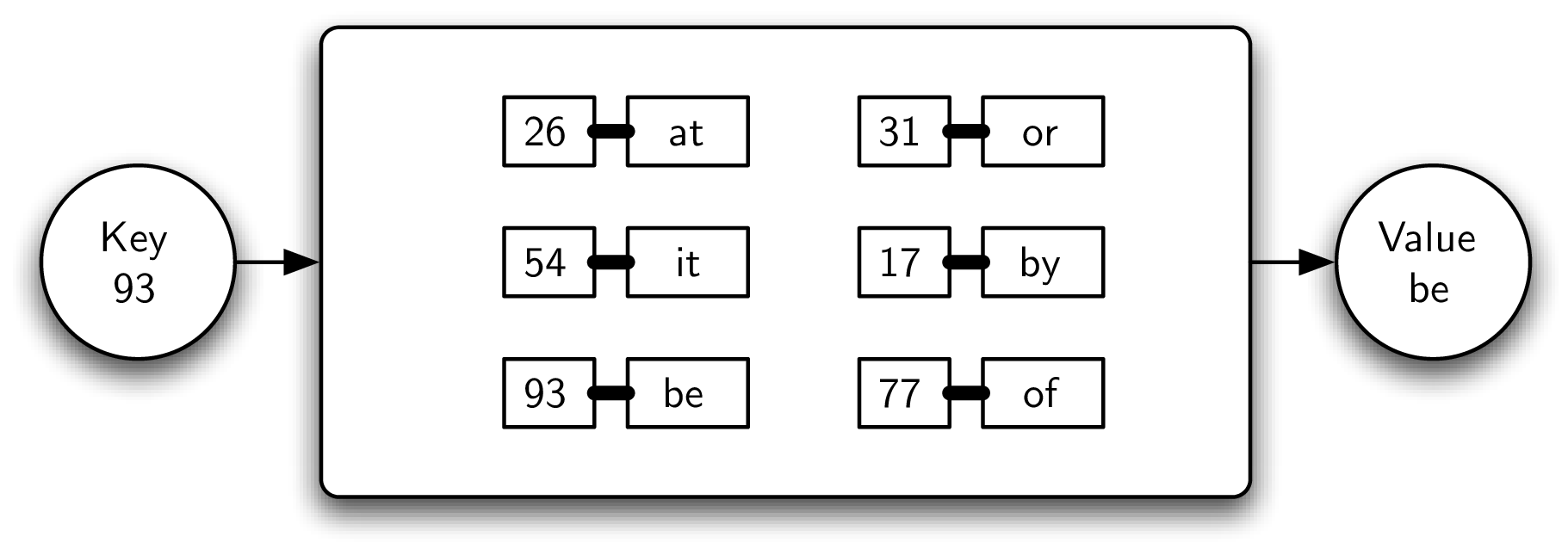
The abilities to put a key-value pair into the map and then look up a data value associated with a given key are the fundamental operations that all maps must provide.

1. Map (ADT)

Map 是一个抽象数据类型，它的定义是：

• a collection of key-value pairs where values can be accessed via their associated key

Operation 包括：

• Constructor: Map()
• 增加新的键值对：put(key, value) 当 map 中不存在同样的 key 时，把这个新的键值对加进去；
• 查找：get(key) 在 map 中查找这个 key，返回对应的 value
• ……

2. Implementing a Dictionary in Python

我们可以用 hash table 来实现 Map，我们把 key 用 hash function 来 hash，然后把这些 key 放在一个 collection 里面，方便我们 search 和 retrieve value。

这种查找方法的时间复杂度大概是 O(1)，但是根据我们的 table size，collision 以及 collision resolution strategy 可能会稍有不同。

Our analysis showed that this technique could potentially yield a 𝑂(1)O(1) search. However, performance degraded due to issues such as table size, collisions, and collision resolution strategy.

我们在讲树结构的时候也说过可以用二叉查找树来实现 Map，key-value pair 就是一个 node，当树平衡的时候查找时间复杂度大概是 $O(log^n)$，但是显然，当树不平衡的时候，我们的查找效率就会降低。

如何避免以上实现方式的缺点呢？

隆重推出一个新的数据结构—— skip list（跳表）。

3. Skip List 跳表

Skip List 是什么？

它是一种 Probabilistic data structures。

概率数据结构（Probabilistic data structures）是一组数据结构，它们对于大数据和流式应用来说非常有用。 一般而言，这类数据结构使用哈希函数（Hash function）来随机化并紧凑地表示一个项的集合。 忽略掉碰撞（Collision）的情况，但错误可以在一定的阈值下得到很好的控制。

先来张图感受一下。

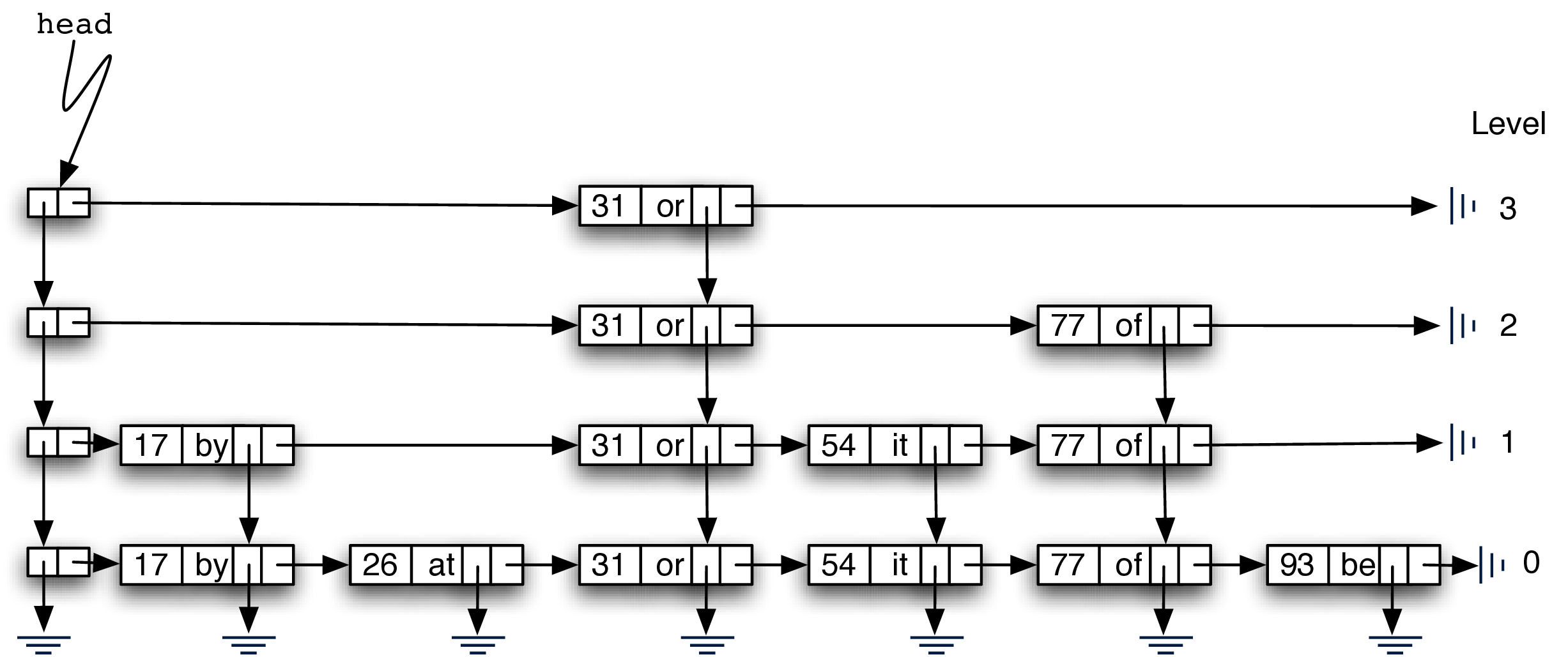
跳表就是一个 2d linked list，link 可以向右或者向下走；

list 的 head（头）在左上角，这是唯一的跳表入口。

A skip list is basically a two-dimensional linked list where the links all go forward (to the right) or down. The head of the list can be seen in the upper-left corner. Note that this is the only entry point into the skip list structure.

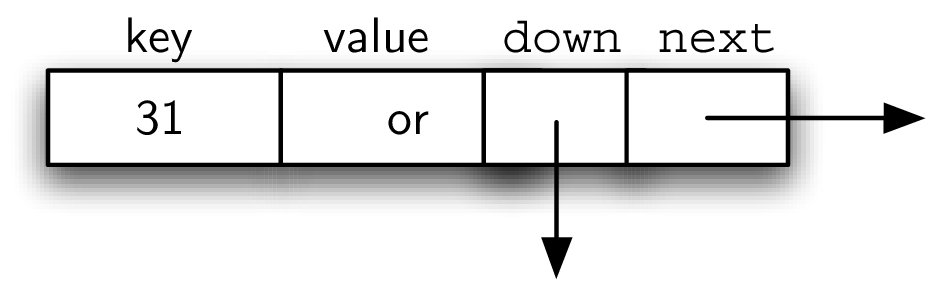
##组成元素：Data Node

• holds key and associated value
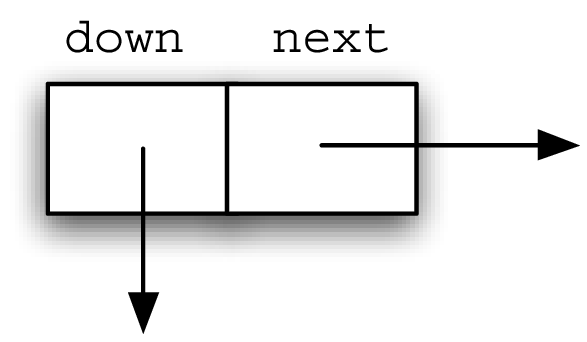
• 每个data node 有两个reference，一个向下，一个向右

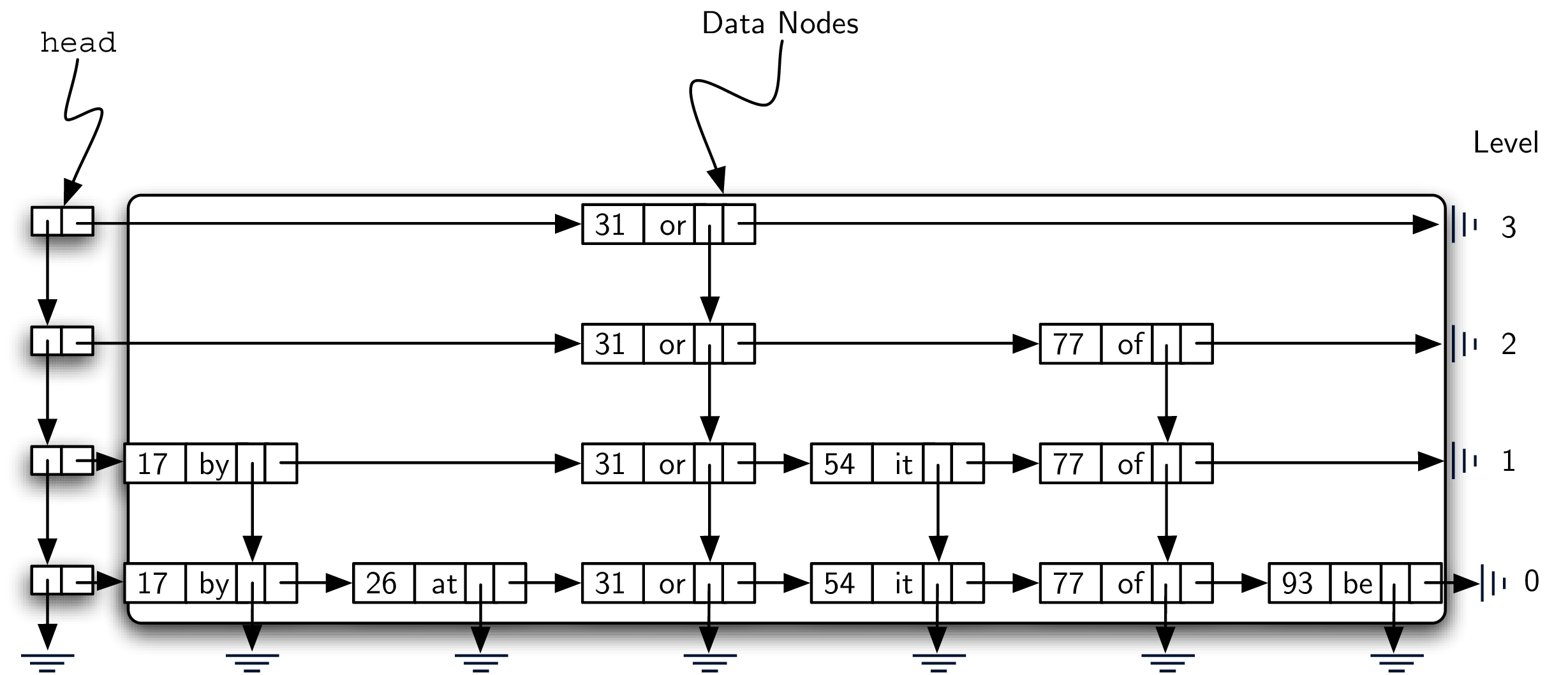
组成元素：Header Nodes

这幅图的左边和中间各有一个框框，左边的框里面包含的是 a linked list of header nodes.

Header nodes 只有两个 reference - down and next.

next 指向 a linked list of data nodes.

down 指向 the next lower header node.

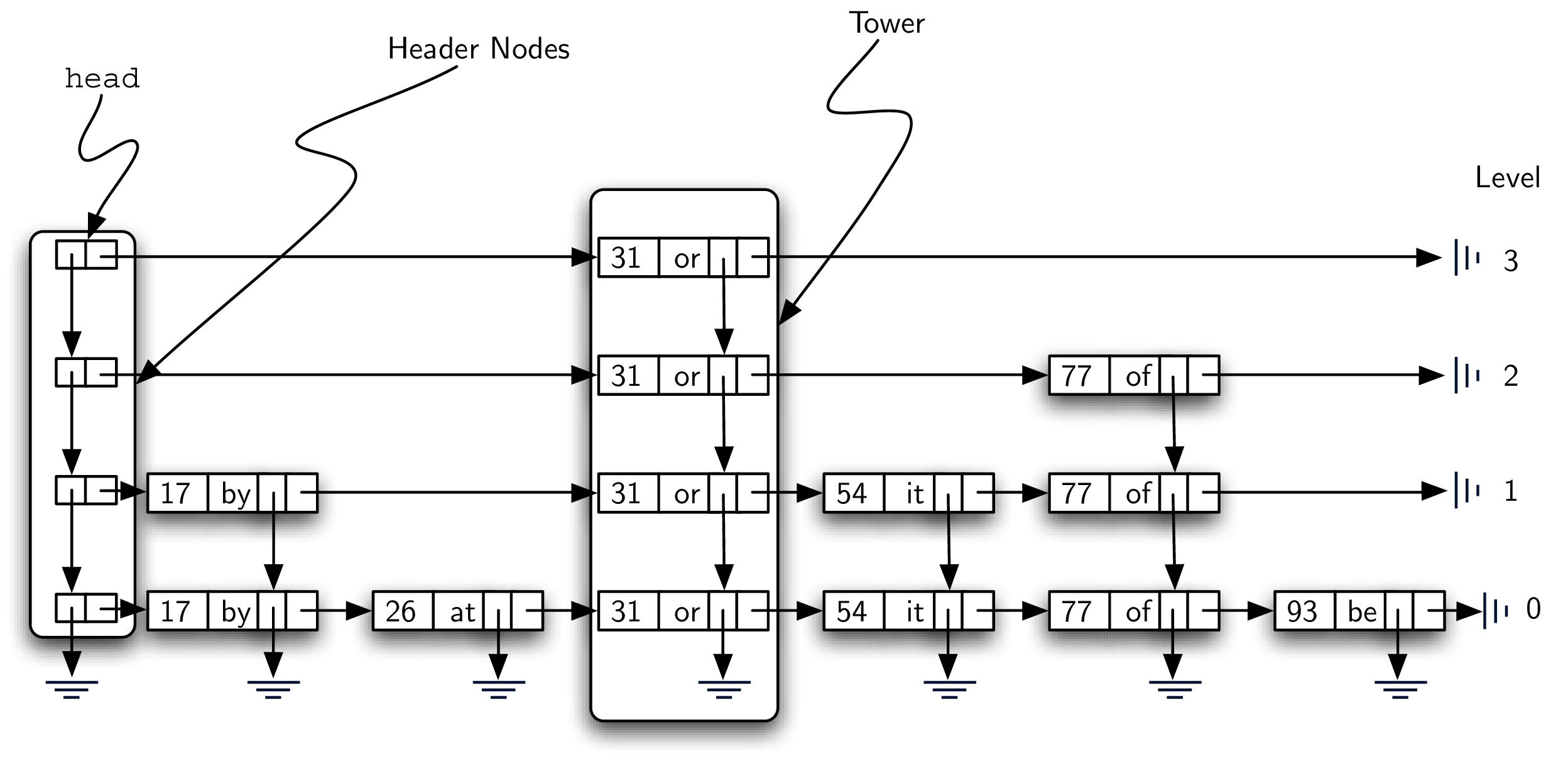
Towers

上图的中间框框包含一系列 data nodes，这个 column 就被称为 tower（想象一下 excel 的表格，是不是很像）。

• tower 是被 data node 的 down reference 联系在一起的；
• tower 的高度可能是不同的；

Towers are linked together by the down reference in the data node.

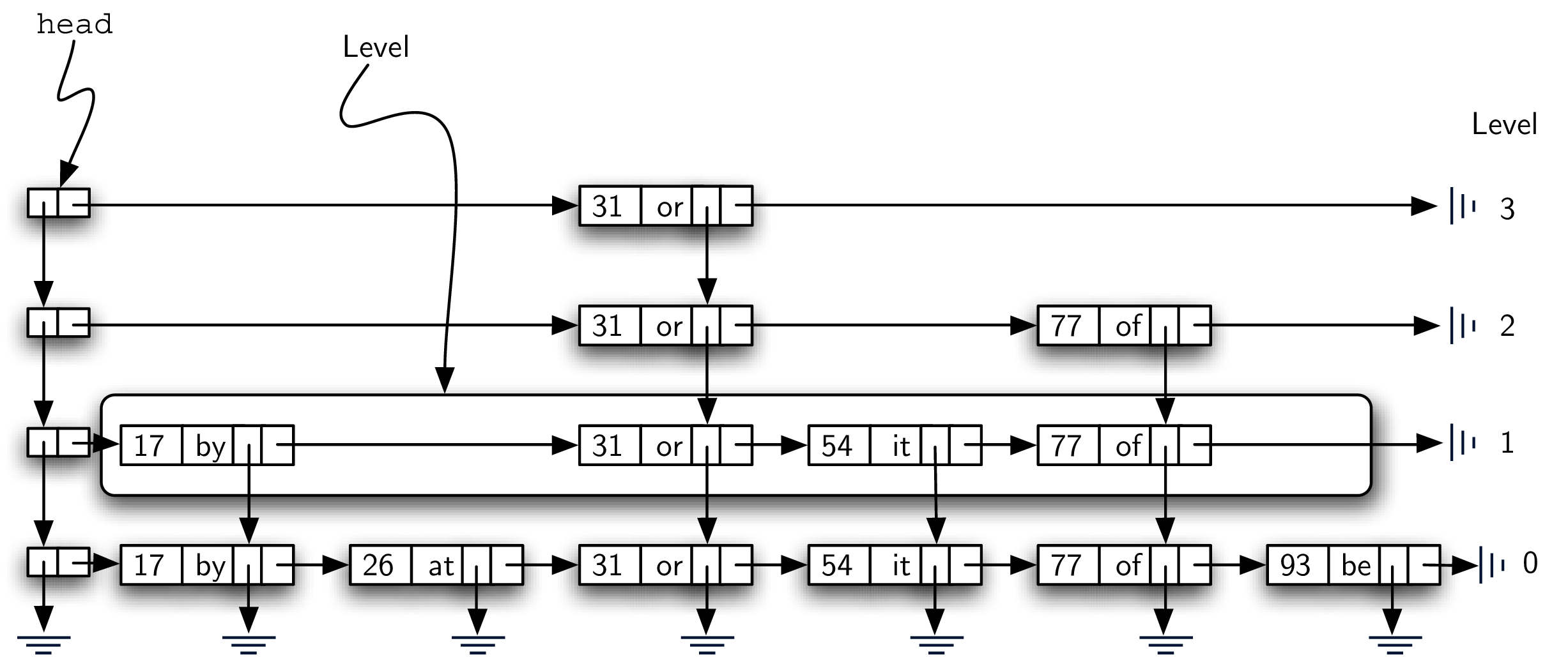
Level

每个横向的 collection 其实就是一个 ordered linked list of data nodes。

• 排序是用 key 来排序的；

• 我们把这种 collection 叫做 level，level 从 0 开始，0 是底层；

• level 0 是一个包含所有 node 的 collection；

• 当我们往 level 更高一点走的时候，我们的 node 数量会减少（注意！！！），这也是 skip list 的一个重要特性，能帮助我们更有效地进行查找；

• 每个 level 的 node 数量是直接跟 tower 的高度相关的。

Levels are named starting with 0 at the lowest row. Level 0 consists of the entire collection of nodes. Every key-value pair must be present in the level-0 linked list. However, as we move up to higher levels, we see that the number of nodes decreases. This is one of the important characteristics of a skip list and will lead to our efficient search. Again, it can be seen that the number of nodes at each level is directly related to the heights of the towers.

4. Skip List - Code

两种 node （HeaderNode 和 DataNode）的实现方式和之前学的 simple linked list 相似，reference 一开始都是 None。

SkipList 的 constructor 只需要设置一个 head，初始化为 None。

When a skip list is created there are no data and therefore no header nodes. The head of the skip list is set to None. As key-value pairs are added to the structure, the list head refers to the first header node which in turn provides access to a linked list of data nodes as well as access to lower levels.

class HeaderNode:
    def __init__(self):
        self._next = None
        self._down = None

    @property
    def next(self):
        return self._next

    @property
    def down(self):
        return self._down

    @next.setter
    def next(self, value):
        self._next = value

    @down.setter
    def down(self, value):
        self._down = value
        
class DataNode:
    def __init__(self, key, value):
        self._key = key
        self._data = value
        self._next = None
        self._down = None

    @property
    def key(self):
        return self._key

    @property
    def data(self):
        return self._data

    @property
    def next(self):
        return self._next

    @property
    def down(self):
        return self._down

    @data.setter
    def data(self, value):
        self._data = value

    @next.setter
    def next(self, value):
        self._next = value

    @down.setter
    def down(self, value):
        self._down = value

class SkipList:
    def __init__(self):
        self._head = None

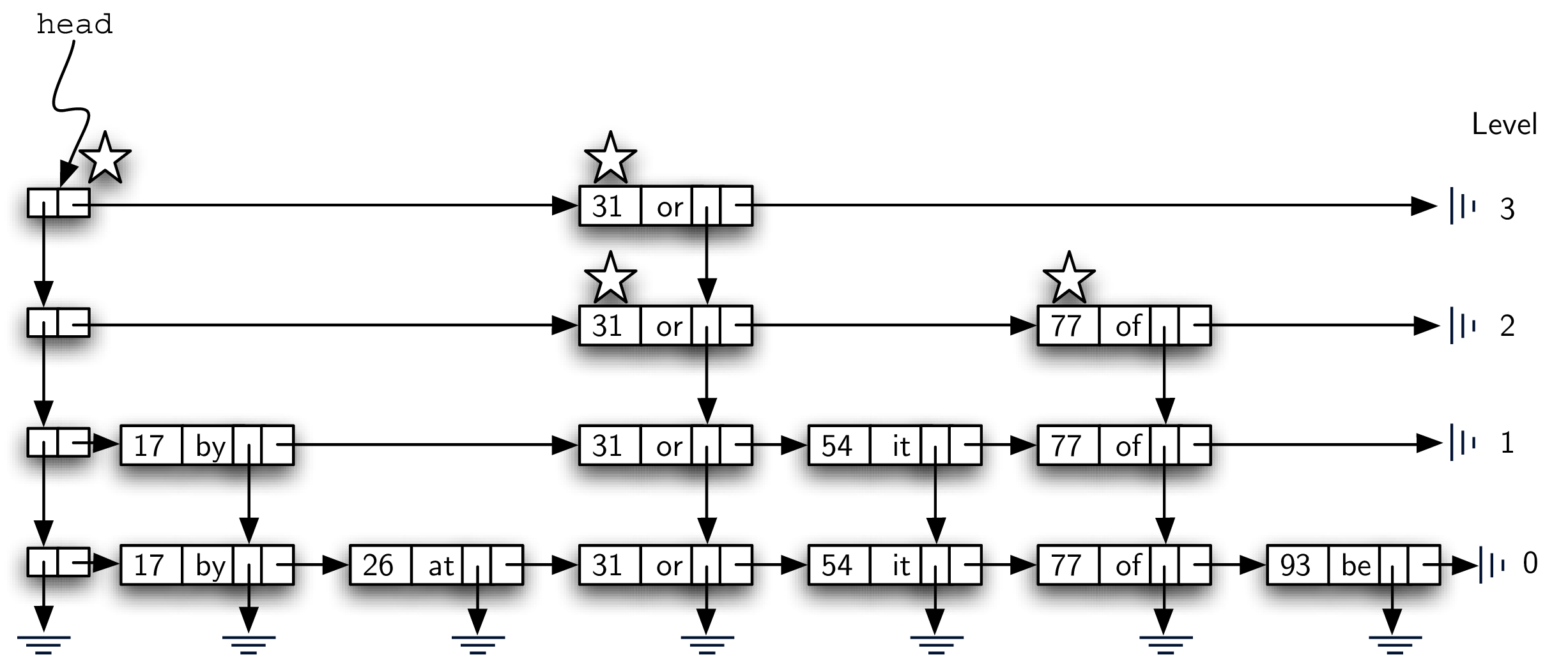
5. Searching a Skip List

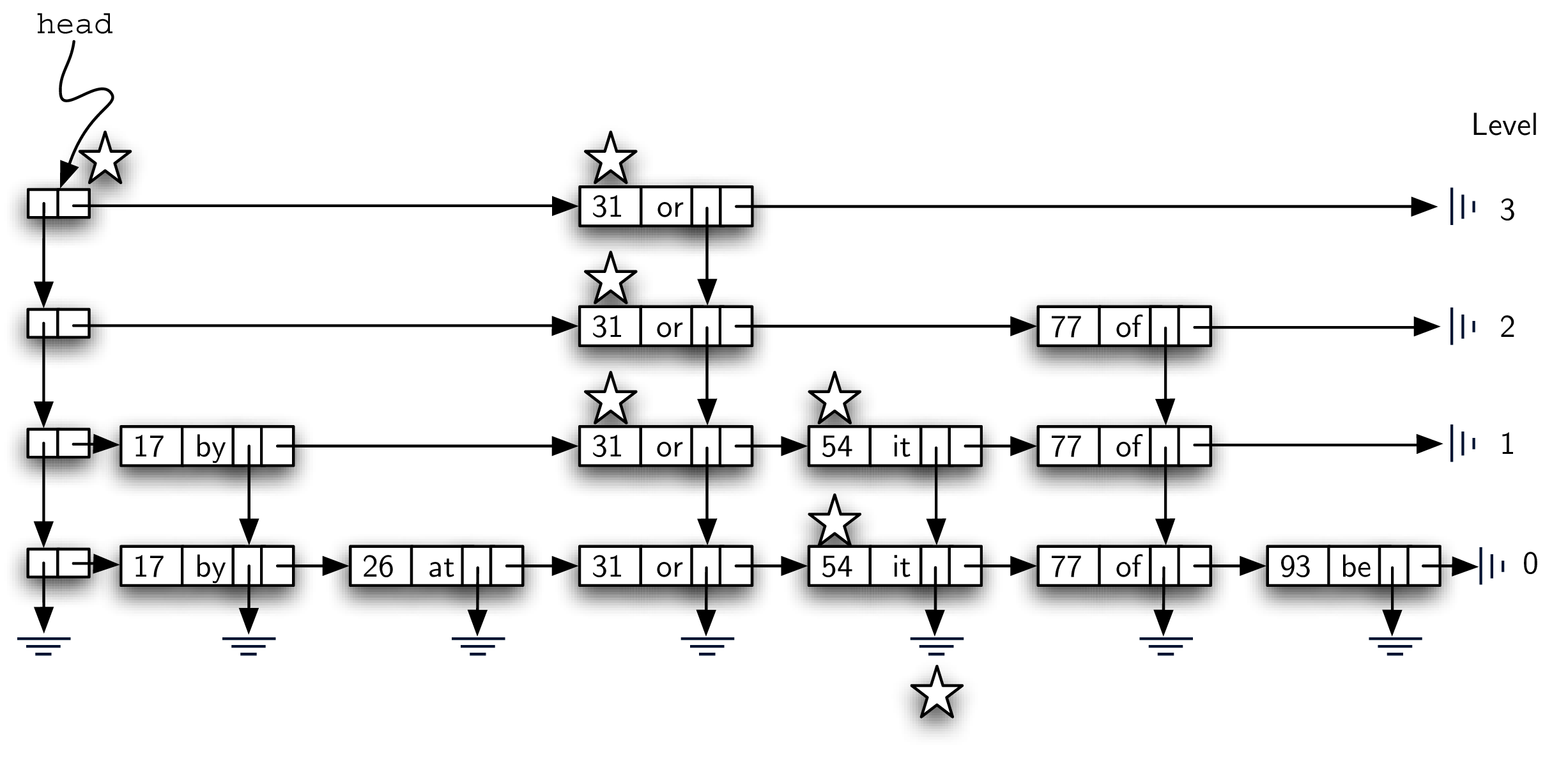
下图展示了找 key=77 的值的过程（带星星的是经过的 node）。

1. start with head node
2. go horizontal - key=31, 31<77 => move forward
3. there’s no node from 31 at level 3, drop down to level 2
4. look to the right, node with key=77 => search successfully found node
5. return “of”

这个过程中，31 < 77 这个对比，让我们可以跳过 17 和 26 这两个 node，我们也不需要经过 lv 1 的 54，直接在 lv 2 就能找到想要的 node，通过分层的方法，我们的查找效率大大提高了！！

Note: 只有 level 0 才包含所有 node。

Since each level is an ordered linked list, a key mismatch provides us with very useful information.

Code

假如 current next 是 None，向下；

假如 current next 是 search key，return data；

假如 current next key > search key，向下；

假如 current next key <= search key，向前；

def search(self, key):
    current = self._head

    while current:
        if current.next is None:  
            current = current.down
        else:
            if current.next.key == key:
                return current.next.data
            else:
                if key < current.next.key:
                    current = current.down
                else:
                    current = current.next
    return None

6. Adding Key-Value Pairs to a Skip List

那么问题来了，怎么构造这样一个 Skip List 呢？

如何把一个新的 key-value pair 加入 Skip List 中呢？

假设这个 key 不存在，我们要加入 key = 65，需要两步：

1. search skip list，找到这个新 key 应该所在的位置（就是做一次 search）；

   我们最终会到达 level 0

2. 然后 create a new data node，加入 level 0 的 linked list 里面

3. 同时我们还要记录整个查找的路径（利用 stack），方便我们在 insert 的时候把经过的 level 都加上新的 data node

The height of the tower for the new entry will not be predetermined but instead will be completely probabilistic. In essence, we will “flip a coin” to decide whether to add another level to the tower. Each time the coin comes up heads, we will add one more level to the current tower.

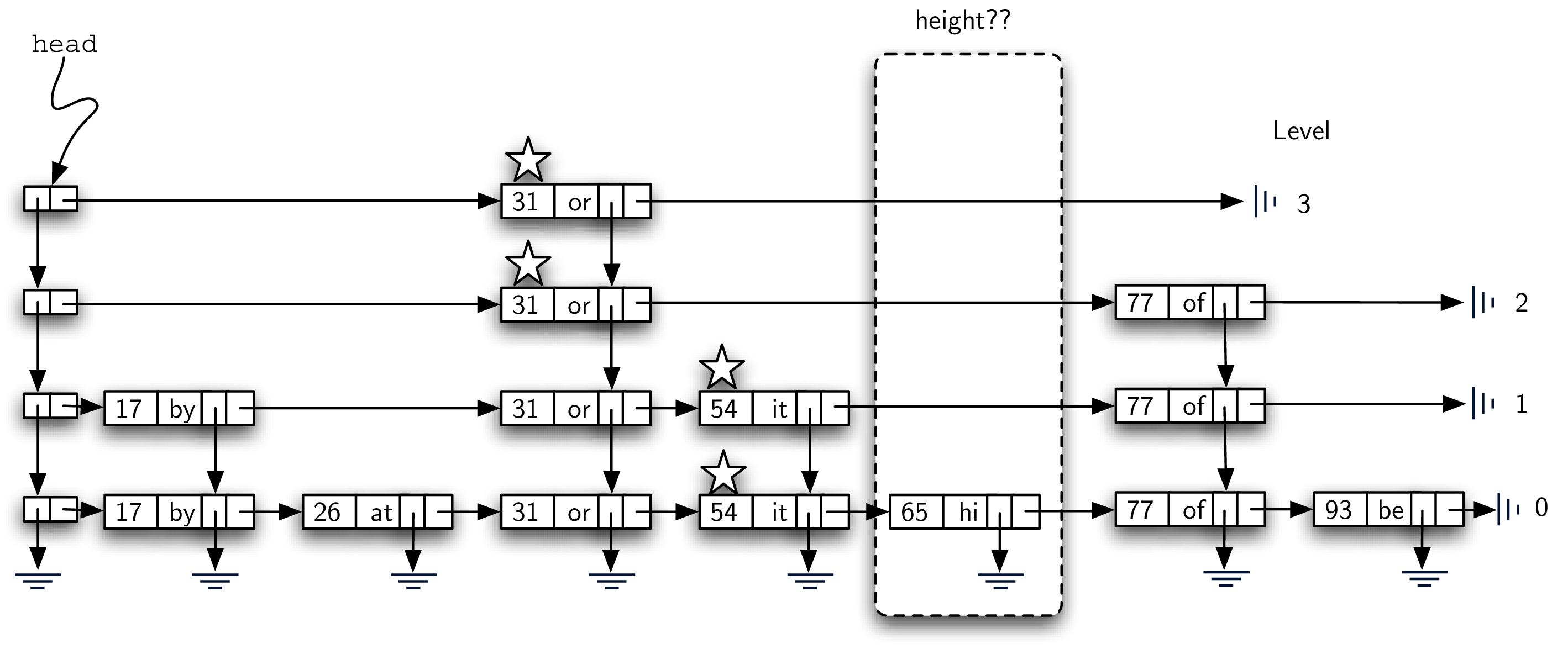
Tower 高度 - 模拟抛硬币

return 1 => heads

return 0 => tail

每次加一个 level，我们都需要加一个 header node。

因为这个随机性的存在，即使 key 一样，我们每次生成的跳表也可能是不同高度的。

Each time a new level is added to the tower, a new data node and a new header node are created. Depending on the random nature of the coin flip, the height of the towers for any particular key is bound to change each time we build the skip list.

from random import randrange
def flip():
    return randrange(2)

Code for inserting new data node

def insert(self, key, value):
    if self._head is None:
        self._head = HeaderNode()
        temp = DataNode(key, value)
        self._head.next = temp
        top = temp
        while flip() == 1:
            if tower.is_empty():
                newhead = HeaderNode()
                temp = DataNode(key, value)
                temp.down = top
                newhead.next = temp
                newhead.down = self._head
                self._head = newhead
                top = temp
            else:
                next_level = tower.pop()
                temp = DataNode(key, value)
                temp.down = top
                temp.next = next_level.next
                next_level.next = temp
                top = temp
    else:

Code (TBC)

This time we pop the insert stack to get the next higher insertion point as the tower grows. Only after the stack becomes empty will we need to return to creating new header nodes.

# 这段代码感觉有点奇怪...
tower = Stack()
current = self._head
while current:
    if current.next is None:
        tower.push(current)
        current = current.down
    else:
        if current.next.key > key:
            tower.push(current)
            current = current.down
        else:
            current = current.next

lowest_level = tower.pop()
temp = DataNode(key, value)
temp.next = lowest_level.next
lowest_level.next = temp
top = temp

7. Building the Map

之前提到 Map 的两个核心 function 就是 insert + search（也就是 put 和 get），我们已经用 Skip List 实现了这两个功能，现在我们可以来实现 Map 了。

class Map:
    def __init__(self):
        self.collection = SkipList()

    def put(self, key, value):
        self.collection.insert(key, value)

    def get(self, key):
        return self.collection.search(key)

8. Analysis of a Skip List

用 ordered linked list 来存 key-value pair 的时候，Search 的时间复杂度是 O(n)，那么 Skip List 的时间复杂度是否更低一些呢？

因为 Skip list 是个概率数据结构，所以在分析复杂度的时候我们也只是做一个大概的分析。

因为 flip = 1 的概率是 1/2，每个 node 的高度至少是 1，我们总共有 n 个 node，那么 node 的 tower 高度为 1 的可能性是 1，高度为 2 的可能性是 n/2，高度为 3 的可能性是 n/4，以此类推。

Tower 的最大高度 = $log2^n + 1$，用 big O 来表示就是 $O(logn)$.

Search method

我们在 search 的时候会向下走和向右走，worst case 就是走到底层 $O(logn)$才能找到 key，而每个 level 横向查找的 node 是一个常数（详细解释见英文），所以 search 的效率是$O(logn)$。

We drop down a level when one of two events occurs. Either we find a data node with a key that is greater than the key we are looking for or we find the end of a level.

If we are currently looking at some data node, the probability that one of those two events will happen in the next link is 1/2. This means that after looking at 2 links, we would expect to drop to the next lower level (we expect to get heads after two coin flips).

Insert method

因为 insert 和 search 的操作基本一样（需要先找到位置），所以它的时间复杂度也是$O(logn)$。

9. 结语

Maps (dictionaries) are associative memory organization structures.