Luna Tech

Tutorials For Dummies.

Recursive: cryptography (1)

2021-05-25

0. 前言

Reference: 9.5

cryptography（密码学）在互联网上使用的非常广泛。每次你登录到一个网站，都会用到 cryptography。

一般来说，密码学能加密和解密你不希望别人看到的一些信息。

今天我们就来看看每天用到的一些 cryptographic programming function。

这些 function 可能会有一些更高效的实现方式，但它们都能通过 recursive 实现，我们接下来讲的就是它们具体的 recursive 实现方式。

1. Modulo Operator

我们会用到 modulo operator (%)，也就是取两数相除之后的余数。

密码学最初只用到了 modulo 运算，比如一个加密字符串 “uryybjbeyq” 是通过下面这个 function 得到的。

def encrypt(m):
    s = "abcdefghijklmnopqrstuvwxyz"
    n = ""
    for i in m:
        j = (s.find(i) + 13) % 26
        n = n + s[j]
    return n

这个 encryte function 用到了一种叫做 “Caesar Cipher“ 的加密方法，也有人把它称作 rot13。

我们把每个字母在字母表 (s) 中的 index 都加上 13，然后再除以 26 (wrap around function)，确保我们最后得到的 index 还是在 0-25 之间的。

因为有 26 个字母，所以这个 function 是对称的（symmetric），这种对称性让我们可以用这个 function 进行信息的加密和解密。

In addition, since there are 26 letters in the alphabet, this function is symmetric. The symmetry allows us to use the function to encrypt and decrypt the same message. If you pass the string "uryybjbeyg" to the encrypt function it returns "helloworld".

Why 13?

我们为什么一定要加 13 呢？

13 是 26/2 的结果，也是它保证了上述 encrypt function 的对称性。

假如我们换一个数字，就会导致不对称（asymmetry），我们需要另外再写一个 decrypt function 去做解密。

Asymmetry would require us to write a separate decrypt algorithm that subtracted the amount to rotate.

# m: message
# k: encryption rotate number
# (26-k): decrypt rotate number

def encrypt(m, k):
    s = "abcdefghijklmnopqrstuvwxyz"
    n = ""
    for i in m:
        j = (s.find(i) + k) % 26
        n = n + s[j]
    return n

def decrypt(m, k):
    s = "abcdefghijklmnopqrstuvwxyz"
    n = ""
    for i in m:
        j = (s.find(i) + 26 - k) % 26
        n = n + s[j]
    return n

安全性

即使别人不知道 k 的值，这种简单的 rotation 加密也是非常容易被破解的。

我们接下来会看一种更加安全的算法：RSA 公钥加密算法（RSA public key encryption algorithm）。

2. Modular Arithmetic Theorems 同余定理

假如 a, b 两个数字在除以 n 之后得到了相同的余数，那么我们就说 a 和 b 是 n 的同余数（congruent modulo）。

我们可以用下面的符号来表达 a 和 b 的关系：

我们即将要学习的算法用到了以下三个重要的定理：

  1. If 𝑎≡𝑏 (mod 𝑛) then ∀𝑐, 𝑎+𝑐≡𝑏+𝑐 (mod 𝑛).
  2. If 𝑎≡𝑏 (mod 𝑛) then ∀𝑐, 𝑎𝑐≡𝑏𝑐 (mod 𝑛).
  3. If 𝑎≡𝑏 (mod 𝑛) then ∀𝑝, 𝑝>0, $𝑎^𝑝$≡$𝑏^𝑝$ (mod 𝑛).

∀ - for all

Modular Exponentiation （模密）

模幂 （英语：modular exponentiation ）是一种对模进行的幂运算，在计算机科学，尤其是公开密钥加密方面有一定用途。

假如我们想要知道 $3^{1254906}$ (mod p) 的最后一位数字，我们关心的只是最后一位，并不需要真的计算出全部的数字。

这个问题可以被抽象为：首先计算出 $x^n$，然后计算出 $x^n$ (mod p) 。

我们可以利用上面提到的第三条定理：

步骤

首先，把 result intialize 为 1；

然后，重复 n 次：

The above approach makes the computation simpler because we are keeping the result smaller rather than following it out to its full precision. However, we can do even better using a recursive approach.

进阶版（递归）

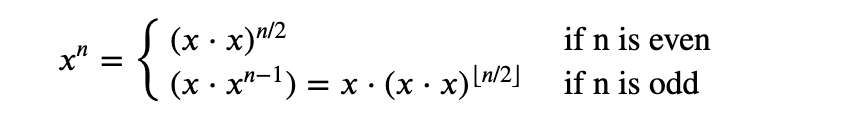
Remember that for a floating point number 𝑛 the floor operation, ⌊𝑛⌋, results in the largest integer smaller than 𝑛.

对于一个浮点数来说，floor operation 的结果是比 n 小的最大 integer。

Python’s integer division operator returns the floor of the result of the division, so we do not need to do anything special in our code to achieve the results we want.

Python 的整数除法运算会返回结果的 floor result，所以我们直接用就行了。

The above equation gives us a very nice recursive definition for computing $𝑥^n$. All we need now is a base case.

上面的等式给了我们一个很好的递归定义，现在我们只需要一个 base case。

已知任何数字的 0 次方都等于 1，而我们在每次递归 function 里都把 n 除以 2，所以 check n = 0 可以作为我们的 base case。

我们也注意到，上面的等式中不管 n 是奇数还是偶数，都包含 $ (𝑥⋅𝑥)^{⌊𝑛/2⌋}$，所以我们在任何情况下都需要计算这个算式，并且把结果存在 tmp variable 里面。

Also note that since we are computing modulo p we still apply the modulo operator at each step of the calculation. The solution in keeps the result size small and uses many fewer multiplications than a purely iterative approach.

同时，我们每一次计算都会用到 modulo operator，这是为了让结果保持一个尽量小的 size，尽量少用乘法。

def modexp(x, n, p):
    if n == 0:
        return 1
    t = (x * x) % p
    tmp = modexp(t, n // 2, p)
    if n % 2 != 0:
        tmp = (tmp * x) % p
    return tmp

3. 最大公约数 The Greatest Common Divisor

Multiplicative Inverses 模反元素/模倒数/模逆元

如果两个正整数 x 和 m 互质，那么一定可以找到整数 b，使得 bx - 1 被 m整除，或者说 bx 被 m 除的余数是 1。

这时，b 就叫做 x 对模数 m 的“模反元素”。

A multiplicative inverse of a positive integer 𝑥 modulo 𝑚 is any number 𝑎 such that 𝑎𝑥≡1(mod 𝑚).

正整数 x 除以 m 取余数的模反元素是 a，a 乘以 x 和 1 是同余数。

比如：x = 3，m = 7，a = 5

3 * 5 = 15，15 % 7 = 1

5 就是 3 除以 7 取余（3）的一个模反元素。

这个概念看起来很让人迷惑，为什么我们要选择 5 呢？5 是 3 除以 7 取余的唯一一个模反元素吗？任何数字 a 都有对于任何数字 m 的一个模反元素吗？

我们来看一下下面的例子：

for i in range(1, 40):
    if (3 * i) % 7 == 1:
        print i # 5,12,19,26,33

这个例子让我们知道3 除以 7 取余（3）的模反元素不止一个，但每个模反元素都满足 n * 7 - 2

所有数字都有模反元素吗？

Do all pairs of numbers 𝑥 and 𝑚, have a multiplicative inverse?

我们再来看一个例子，假设 x = 4, m = 8。

代入前面的代码，我们没有得到任何的 output。

(4*i)/8 的结果只能是 0 或者 4，不可能是 1。

那么，到底哪些数字有模反元素呢？

The answer is that a number 𝑥 has a multiplicative inverse, modulo 𝑚, if and only if 𝑚 and 𝑥 are relatively prime.

当且仅当 m 和 x 都互为质数/素数的时候，x 对于 m 有模反元素。

那么，哪些数字互为质数呢？

当两个数字的最大公约数为 1。

Two numbers are relatively prime if 𝑔𝑐𝑑(𝑚,𝑥)=1

4. 我们如何计算两个数字的最大公约数呢？

欧几里得算法

Given two numbers 𝑎 and 𝑏 we can find the GCD by repeatedly subtracting 𝑏 from 𝑎 until 𝑎<𝑏. When 𝑎<𝑏, we switch roles for 𝑎 and 𝑏. At some point 𝑎−𝑏 becomes 0, so we swap 𝑎 and 𝑏 one more time. At that point we have 𝑔𝑐𝑑(𝑎,b)=𝑎. This algorithm was first described more than 2,000 years ago and is called Euclid’s Algorithm.

假如我们要找 a 和 b 的最大公约数，那么我们把较大的数字作为 a，较小的数字作为 b。

比如计算 3 和 7 的最大公约数：

  1. a = 7, b = 3
  2. a - b = 7 - 3 = 4，a = a - b = 4
  3. 因为 4 > b，所以计算 4 - b = 4 - 3 = 1
  4. 因为 1 < b，所以互换 a 和 b，a = 3, b = 1
  5. 计算 a - b = 2，a = 2，b = 1
  6. 因为 2 > 1，所以计算 2 - 1 = 1,
  7. 此时 a = b = 1，a - b = 0
  8. a 和 b 互换（这里换不换都一样，都是1），所以 3 和 7 的最大公约数为 1，两数互为质数
def gcd(a, b):
    if b == 0:
        return a
    elif a < b:
        return gcd(b, a)
    return gcd(a - b, b)

上面的算法可以优化为辗转相除法。

辗转相除法

辗转相除法基于如下原理：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。

辗转相除法是一种递归算法，每一步计算的输出值就是下一步计算时的输入值。

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

5. 计算模反元素

假设有 x 和 y 两个数字以及 a 和 b 两个整数，x 和 y 的最大公约数是 d，那么根据同余定理的第一条：𝑑=𝑔𝑐𝑑(𝑥,𝑦)=𝑎𝑥+𝑏𝑦。

比如 1=𝑔𝑐𝑑(3,7)=−2×3+1×7，a 和 b 分别为 -2 和 1.

那么换个字母表示也一样：1=𝑔𝑐𝑑(𝑚,𝑥)=𝑎𝑚+𝑏𝑥

m = 3, x = 7, a = -2, b = 1

𝑏𝑥 - 1 = 1*7 - 1 = 6

(bx -1) mod 𝑚 = 6 mod 3 = 0

所以 1 (b) 是 7 (x) 对于 3 (m) 取余 (7) 的模反元素，或者说：

b 是 x 对模数 m 的模反元素。

6. 欧几里得算法拓展

We have reduced the problem of computing inverses to the problem of finding integers 𝑎 and 𝑏 that satisfy the equation 𝑑=𝑔𝑐𝑑(𝑥,𝑦)=𝑎𝑥+𝑏𝑦.

We will take two numbers 𝑥>=𝑦 and return a tuple (𝑑,𝑎,𝑏) such that 𝑑=𝑔𝑐𝑑(𝑥,𝑦) and 𝑑=𝑎𝑥+𝑏𝑦.

我们现在要计算满足 𝑑=𝑔𝑐𝑑(𝑥,𝑦)=𝑎𝑥+𝑏𝑦 的 a 和 b。

我们的 input 是 x 和 y（x 大于等于 y），然后返回 d，a，b三个值。

d 是 x 和 y 的最大公约数，ax + by 等于 d。

def ext_gcd(x, y):
    if y == 0:
        return (x, 1, 0)
    else:
        (d, a, b) = ext_gcd(y, x % y)
        return (d, b, a - (x // y) * b) # 后面证明

图解拓展算法

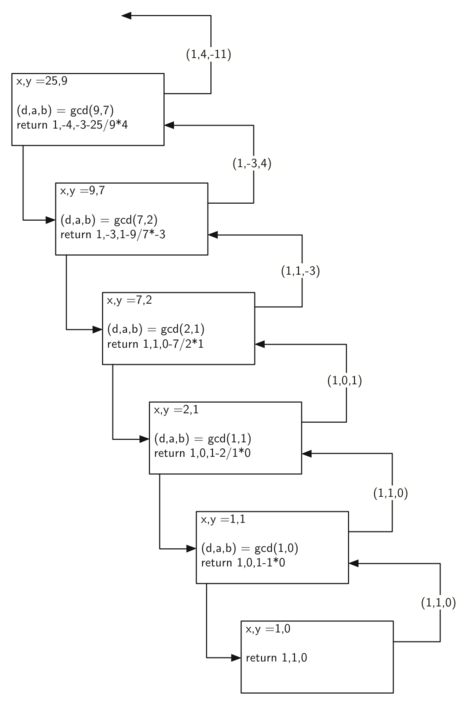
Call Tree for Extended GCD Algorithm

说明

7. 结语

密码学考的就是数学啊……

一开始我看的云里雾里（参考的英文教程写的不是很清楚），后来百度了才发现教程讲的是同余定理、质数、最大公约数（欧几里得算法和辗转相除法）、模反元素这些知识点（看中文的时候觉得很熟悉，看英文则半天都理解不了┭┮﹏┭┮）。

下一篇进入密码学正题：RSA 算法。