Graph: The Word Ladder Problem (2) - BFS

2021-05-03

0. 前言

Reference: 8.9-8.10

上篇讲了 Word Ladder 游戏的两种思路，我们成功地用方法 2（分组法）创建了 Graph，里面包含了我们完成游戏的必要信息：所有的 word 以及 word 相差一个字母的联系。

现在游戏开始啦！给定一个 start word 和 end word，你需要用最少的 transformation 来完成转换。

这个游戏规则翻译一下，就是找到最短路程——shortest path。

我们怎么找呢？有一个算法叫做 Breadth first search (BFS)，它是一种简单的、搜索 graph 的算法，基于 BFS 人们还开发了很多其他的算法（元老级啊~），所以我们就先来学习一下 BFS 吧！基础打好，后面其他的算法就不虚啦~

1. Breadth First Search 逻辑

给定一个 graph G和 starting node s，BFS 会先查找这个 node s 所有的 edge，从距离短的开始找，找完了距离=k 的再找距离=k+1 的。

为了记住自己找过了哪些 node，BFS 会用三种颜色来进行标记，白、灰、黑。

白色是默认色，代表没有被查找过。
当开始查找这个 node 的 edge 时，颜色就变成灰色（表示开始找了但没有找完）。
当这个 node 所有的 edge 都被查找完以后，颜色就变成黑色。

A gray node, on the other hand, may have some white vertices adjacent to it, indicating that there are still additional vertices to explore.

Queue

用来决定下一个查找的 node ，每当我们遇到一个颜色为白色的 node，就加入到 queue 里面。第一个被加入的 node 是 start node。

Node

node class需要多三个 variable: distance, predecessor, color，才能完成 BFS。

Starting node 的属性：

color: white
distance: 0
predecessor: None

explore 就是遍历 node 的邻接表，遍历的时候邻接表里面的 node 颜色也很重要，假如是白色，就做下面的四件事：

把这个邻接 node 的颜色改成灰色；
把邻接 node 的 predecessor 改成 currentNode
把邻接 node 的 distance 改成 currentNode + 1
把邻接 node 加入 queue 的末尾，当我们遍历完 currentNode 的所有 edge 之后就要遍历这个邻接 node。

2. Implementation

Note

Vertex 和 Node 是一个意思；
StartNode 就是开始查找的那个 node（这个例子中是 fool）；
Traverse 的 input 是 end node（这个例子中是 sage），它会输出我们找到的最短路径（从 fool 到 sage）。

Code

需要先安装这个package哦~ pip3 install pythonds

https://github.com/bnmnetp/pythonds

https://pypi.org/project/pythonds/

# pip3 install pythonds
from pythonds.graphs import Graph, Vertex
from pythonds.basic import Queue

def buildGraph():
    d = {}
    g = Graph()
    wordlist = ['fool','pool', 'foil', 'foul', 'cool', 'poll', 'fail', 'pole', 'pall', 'pope', 'pale', 'page', 'sale', 'sage']
    # create buckets of words that differ by one letter
    for word in wordlist:
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    # add vertices and edges for words in the same bucket
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)
    return g

def bfs(g,start):
  start.setDistance(0)
  start.setPred(None)
  vertQueue = Queue()
  vertQueue.enqueue(start)
  while (vertQueue.size() > 0):
    currentVert = vertQueue.dequeue()
    for nbr in currentVert.getConnections():
      if (nbr.getColor() == 'white'):
        nbr.setColor('gray')
        nbr.setDistance(currentVert.getDistance() + 1)
        nbr.setPred(currentVert)
        vertQueue.enqueue(nbr)
    currentVert.setColor('black')

def traverse(y):
    x = y
    while (x.getPred()):
        print(x.getId())
        x = x.getPred()
    print(x.getId())

g = buildGraph()
startNode = g.getVertex('fool')
bfs(g, startNode)
traverse(g.getVertex('sage'))

图解

1. Start with “fool”

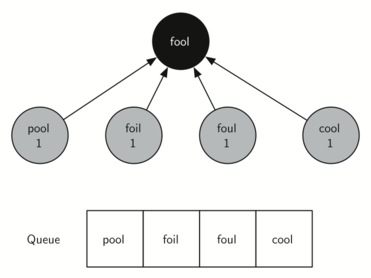
2. Explore all neighbours of “fool”

All neighbours are added into the queue for later exploration.

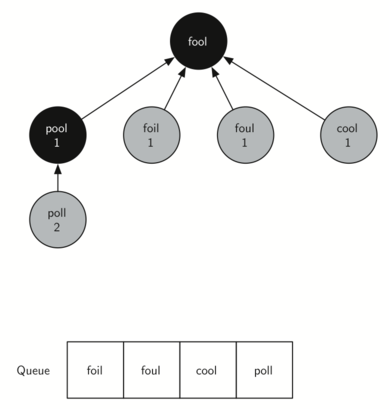
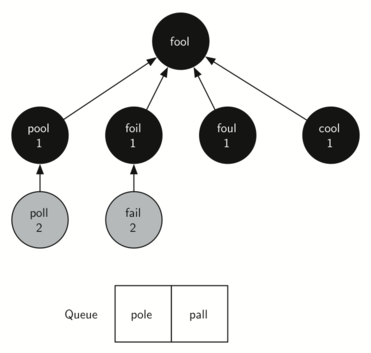
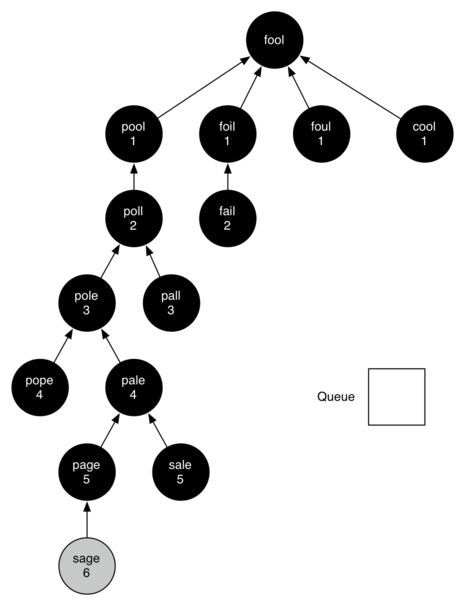
3. Reach the end

No white nodes
Queue is empty

3. Breadth First Search 效率分析

分析 bfs method 的复杂度。

def bfs(g,start):
  start.setDistance(0) # O(1)
  start.setPred(None) # O(1)
  vertQueue = Queue() # O(1)
  vertQueue.enqueue(start) # O(1)
  while (vertQueue.size() > 0): # O(n)
    currentVert = vertQueue.dequeue() # O(1)
    for nbr in currentVert.getConnections(): # O(m)
      if (nbr.getColor() == 'white'): # O(1)
        nbr.setColor('gray') # O(1)
        nbr.setDistance(currentVert.getDistance() + 1) # O(1)
        nbr.setPred(currentVert) # O(1)
        vertQueue.enqueue(nbr) # O(1)
    currentVert.setColor('black') # O(1)

while loop 每个 node 必须遍历一次；
for loop 里面每个 edge 遍历一次；

常数忽略，所以时间复杂度是 O(n+m), n=node总数，m = edge总数。

4. 结语

总结一下，BFS 这个算法用到了三种颜色+一个 Queue 来记录并指导整个遍历的过程。

时间复杂度O(m+n)