Graph: Shortest Path Problems

2021-05-11

0. 前言

Reference: 8.19-8.21

从我们打开浏览器，输入网站，到看到网页这个过程中，发生了很多事情。

我们的设备（电脑）需要把数据经过多个 router 发送给网站，然后网站穿给我们的数据又经过多个 router 到达电脑的浏览器。

mac 用户可以用 traceroute <website address> 得到详细的 routing 信息。

每个 router 都和一个或多个 router 相连，每天的不同时间访问同一个网站，routing 很有可能是不同的。

我们可以把 network of routers 用一个 graph with weighted edges 来表示，edge 的 weight 表示的是两个 router 之间连接的时间。

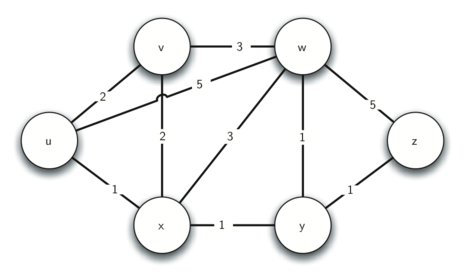
Connections and Weights between Routers in the Internet

我们要解决的问题是：找到从 A router 到 B router 之间时间最短的那条路径。

1. Shortest Path Problems

我们在讲 BFS 的时候，解决的是一个类似的问题：Word Ladder（找到从 A 变成 B 的最短路径）。

Word Ladder 里面的 edge 是没有 weight 这个属性的，假如我们这个 routing 的问题中去掉了 weight，就跟 Word Ladder 的问题一模一样~

最短路径问题有两类：

Weighted Graph - Word Ladder
Unweighted Graph - Routing

2. Dijkstra’s Algorithm

我们用来解决最短路径问题的算法叫做 Dijkstra’s Algorithm（戴克斯特拉算法）

https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm

这个算法的特点是，你只要给定 starting node，它能帮你找到 starting node 到所有其他 node 的最短距离，类似 BFS 的返回结果。

注意：这个算法只有在 edge weight 非负数的情况下才能用。

It is important to note that Dijkstra’s algorithm works only when the weights are all positive. You should convince yourself that if you introduced a negative weight on one of the edges to the graph that the algorithm would never exit.

逻辑

我们用 dist 这个属性来记录从 starting node 到其他 node 的距离，dist 代表从 starting node 到当前 node 的 total weight。
由于图中的每个 node 都要访问，我们用 priority queue 来决定访问 node 的次序，priority queue 的排列是基于 dist 这个属性的。
我们把每个 node 的 dist 初始值设的非常大，算法结束时每个 node 的 dist 都会成为正确的值。

复习

Priority Queue 是基于 Binary Heap 实现的，我们当时实现的那个 PQ 和 Dijkstra 算法的 PQ 有一些不同。

Priority Queue class 存 tuples of key, value pairs, 在 Dijkstra 算法中，Priority Queue 的 key 必须和 node/vertex 的 key 一样；
tuple 里面的 value 是用来决定优先级的，我们用 node/vertex 的 distance 作为优先级；
我们有个额外的 method - decreaseKey，当一个 node 已经在 queue 里面时，这个 method 会被调用，来减少 node 的 dist，因为 dist 变少了，所以这个 node 也会被排到优先队列的前面。

Priority Queue

Code

from pythonds.graphs import PriorityQueue, Graph, Vertex
def dijkstra(aGraph,start):
    pq = PriorityQueue()
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in aGraph])
    while not pq.isEmpty():
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance() \
                    + currentVert.getWeight(nextVert)
            if newDist < nextVert.getDistance():
                nextVert.setDistance( newDist )
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert,newDist)

2. 算法图解

1. 准备工作

Starting node: u
u 有三个邻接 node：v, w, x
三个邻接 node 的初始 dist 是 sys.maxint
新的 dist 是它们跟 start node 之间的 edge 重量

v: d = 2

w: d = 5

x: d = 1
我们把这三个 node 的 predecessor 都设为 u
dist 是 priority queue 的 value

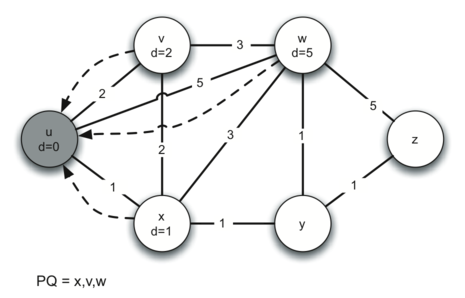
2. while loop

因为 x 的 dist 最小，它在优先队列的最前面，所以我们先看 x 的邻接 node - u, v, w, y.

我们会看一下每个邻接 node 的 dist，从 x 到这些 node 的距离是否比之前已知的 dist 要小，假如是的话就更新 dist。

我们发现 y 的 dist 是初始值 sys.maxint，现在更新为 2 (start node 到 x 再到 y 的距离)。

u 和 v 的距离不需要更新。

w 的距离本来是 5，现在可以减少到 4，我们也更新一下，同时把 w 的 predecessor 改成 x。

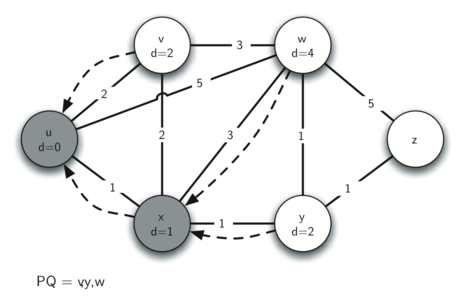
3. 访问 `v`

根据优先队列的顺序，我们访问 v 。

v 的邻接 node 没有什么要改变的 - dist 不需要更新，predecessor 也不需要更新。

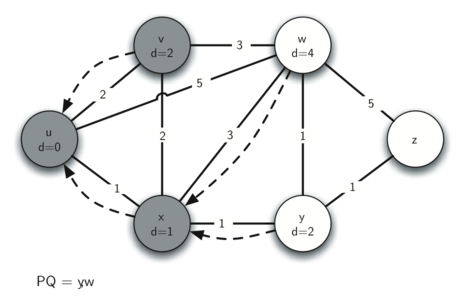
4. 访问 `y`

我们可以更新 w 和 z 的距离和 predecessor。

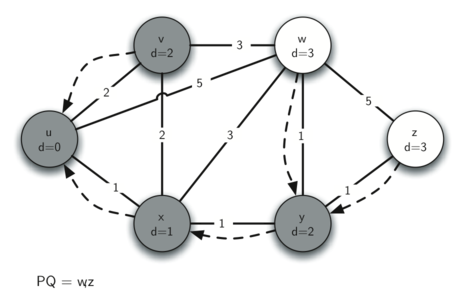
5. 访问 `w`

没有要改的。

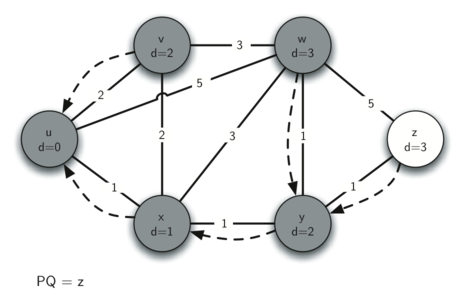
6. 访问 `z`

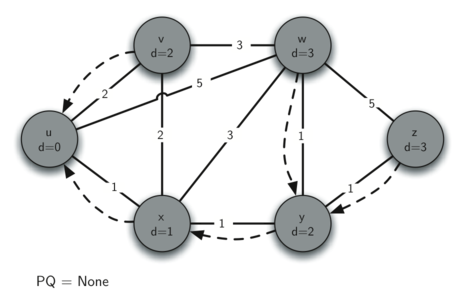
没有要改的，priority queue 为 empty，跳出循环。

4. 算法分析

局限

不支持负数 weight；
你必须有完整的图才能开始计算；

The implication of this is that every router has a complete map of all the routers in the Internet.

不过呢，有其他的算法可以在图不完整的时候进行计算，比如 “distance vector” routing algorithm.

复杂度

build priority queue - O(V)

每个 node 都访问一次
while loop - O(VlogV)

每个 node 都访问一次 - O(V)

在 while loop 里面的 delMin - O(logV)
for loop - 𝑂(Elog𝑉)

每个 edge 一次 - O(E)

for loop 里面的 decreaseKey - 𝑂(log𝑉)

总共的时间复杂度：

O(V)+O(VlogV)+𝑂(Elog𝑉)

= 𝑂((𝑉+𝐸)log(𝑉)).