Leetcode 498 - 对角线遍历(Diagonal Traverse)
2021-09-04
1. 题目
498. 对角线遍历 - 力扣(LeetCode) (leetcode-cn.com)

input: 2d array,也就是一个矩形,我们需要从初始位置开始,进行蛇形游走
output: 代表行走路线的数字的 array
class Solution {
public int[] findDiagonalOrder(int[][] matrix) {
}
}
2. 思路
这道题目需要搞清楚以下几件事:
- matrix 的长度(totalRow)和宽度(totalCol);
- 上行和下行的操作(index 如何变化);
- 转向的条件;
- 转向后如何找到新的 head node;

让我们根据上面的例子来进行一次行走。
| Current Node | Current Position | Next Node | Next Position | Up | Turn |
|---|---|---|---|---|---|
| 1 | 0,0 | 2 | 0,1 | true | true |
| 2 | 0,1 | 6 | 1,0 | false | |
| 6 | 1,0 | 11 | 2,0 | false | true |
| 11 | 2,0 | 7 | 1,1 | true | |
| 7 | 1,1 | 3 | 0,2 | true | |
| 3 | 0,2 | 4 | 0,3 | true | true |
| 4 | 0,3 | 8 | 1,2 | false | |
| 8 | 1,2 | 12 | 2,1 | false | |
| 12 | 2,1 | 16 | 3,0 | false | |
| 16 | 3,0 | 17 | 3,1 | false | true |
| 17 | 3,1 | 13 | 2,2 | true | |
| 13 | 2,2 | 9 | 1,3 | true | |
| 9 | 1,3 | 5 | 0,4 | true | |
| 5 | 0,4 | 10 | 1,4 | true | true |
| 10 | 1,4 | 14 | 2,3 | false | |
| 14 | 2,3 | 18 | 3,2 | false | |
| 18 | 3,2 | 19 | 3,3 | false | true |
| 19 | 3,3 | 15 | 2,4 | true | |
| 15 | 2,4 | 20 | 3,4 | false | true |

上行和下行的规律
我们可以发现,所有的上行都是移动到 [currentRow - 1, currentCol + 1] 的位置,所有的下行都是移动到 [currentRow + 1, currentCol - 1] 的位置。
然后再看什么时候转向,当 currentNode 处于矩形的四条边上而且 next node 的位置 out of boundary 的时候我们就要转向了。
那么转向的时候怎么确定 nextNode 的位置呢?
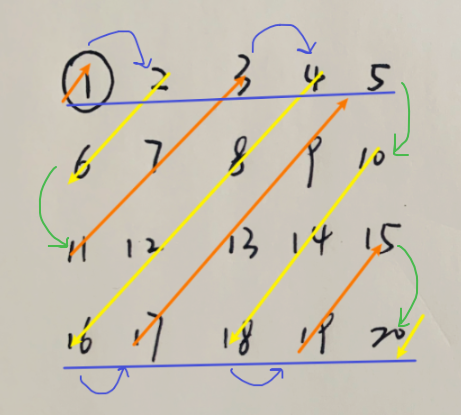
可以分为两种情况:
- 当 currentNode 在矩形的横边时,我们都是向右边平移一格,也就是 [currentRow, currentCol + 1] 这个位置(图中蓝色箭头);
- 反之,我们就是往下移动一格,也就是图中绿色箭头,移动到 [currentRow + 1, currentCol] 这个位置;
注意:转向需要设置 flag 的值。
实现
class Solution {
public int[] findDiagonalOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0)
return new int[0];
boolean goingUp = true;
int totalRow = matrix.length;
int totalCol = matrix[0].length;
int curRow = 0;
int curCol = 0;
int[] result = new int[totalRow * totalCol];
int i = 0; // keep track of result array current index
while (curRow < totalRow && curCol < totalCol) {
// add current node into the result
result[i] = matrix[curRow][curCol];
int nextRow = curRow + (goingUp ? -1 : 1);
int nextCol = curCol + (goingUp ? 1 : -1);
// need to change direction because next node is out of boundary
if (nextRow < 0 || nextRow == totalRow || nextCol < 0 || nextCol == totalCol) {
goingUp = !goingUp;
// node in horizontal edge (not the last one on the edge)
if ((curRow == 0 || curRow == totalRow - 1) && curCol < totalCol - 1 )
curCol += 1;
else
curRow += 1;
}
else {
curRow = nextRow;
curCol = nextCol;
}
i++;
}
return result;
}
}
复杂度
时间复杂度:O(n*m) - 每个元素遍历一次
空间复杂度:O(1) - 常数变量
3. 一些类似的解法
上面的解法是在遍历的时候做转向,有一些其他的解法是类似的,但用的条件不太一样。
参考 1
这个解法没有用到我说的横边右移规则,它是根据 direction 以及当前的 col 和 row value 来判断到底怎么得到下一个 node。
也就是分别判断以下两种情况:
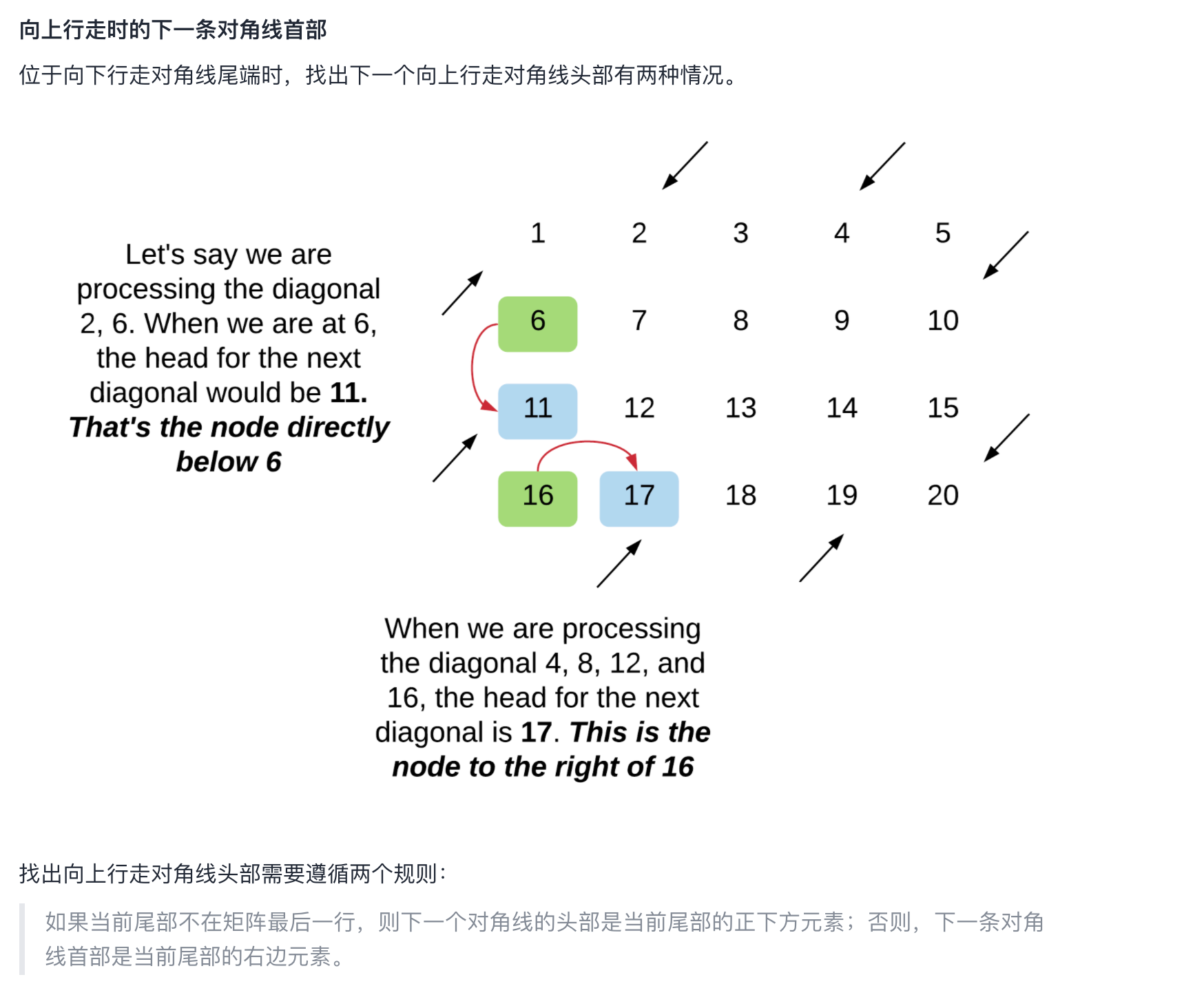
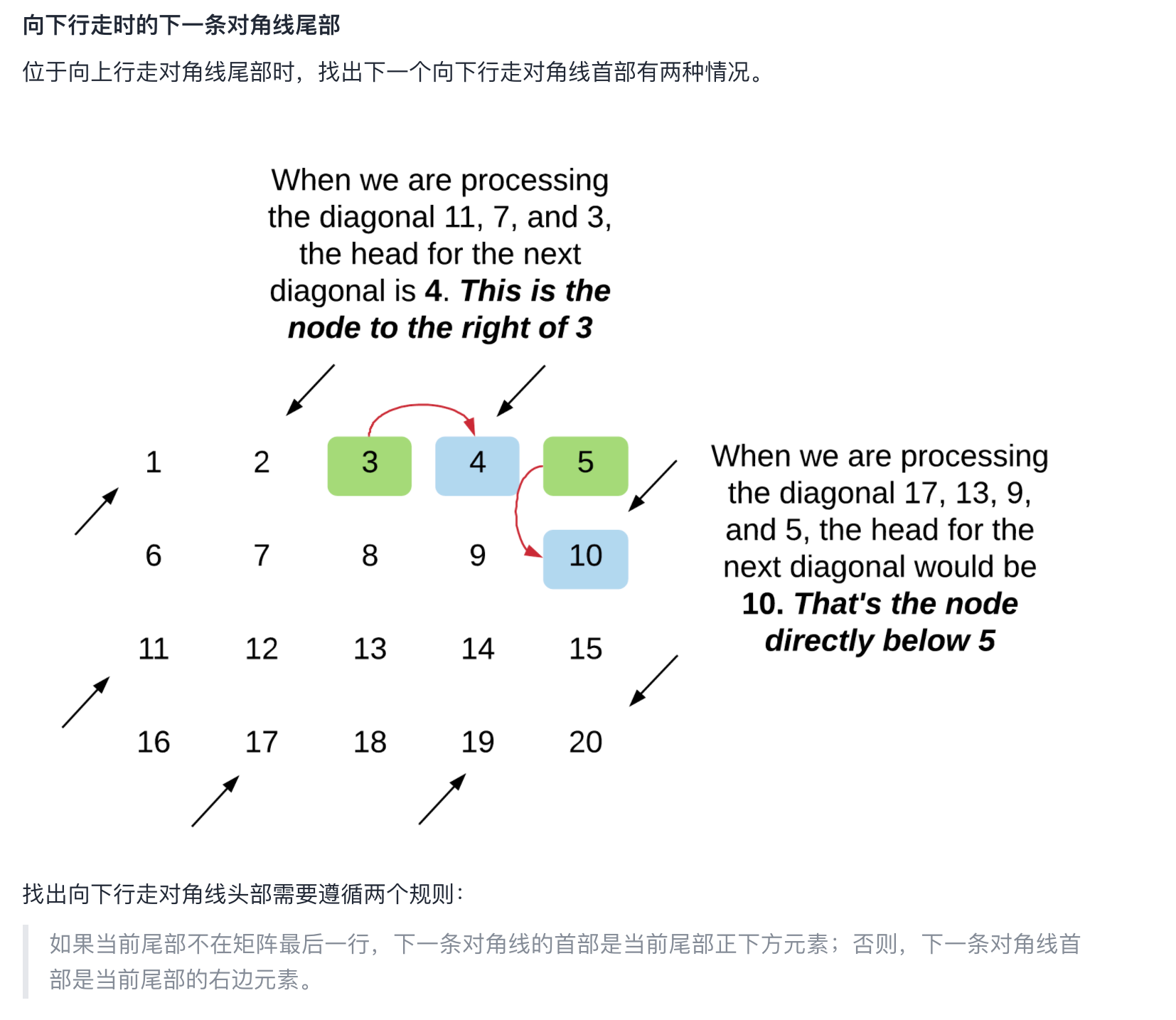
class Solution {
public int[] findDiagonalOrder(int[][] matrix) {
// edge case
if (matrix == null || matrix.length == 0) {
return new int[0];
}
// matrix boundary
int totalRow = matrix.length;
int totalCol = matrix[0].length;
// current node index
int nodeRow = 0, nodeCol = 0;
// 1 = go up
int direction = 1;
int[] result = new int[totalRow*totalCol];
int resultIndex = 0;
// 用 while loop 来确定 iteration 条件
while (nodeRow < totalRow && nodeCol < totalCol) {
// 先用后加,把当前 node 放进 result
result[resultIndex++] = matrix[nodeRow][nodeCol];
// 假如向上,那么 row-1, col+1
// 假如向下,那么 row+1, col-1
int new_row = nodeRow + (direction == 1 ? -1 : 1);
int new_column = nodeCol + (direction == 1 ? 1 : -1);
// 假如满足任意一个条件,表示 out of matrix,需要转向,也就是定义新的 head,同时要改方向
if (new_row < 0 || new_row == totalRow || new_column < 0 || new_column == totalCol) {
// 正在向上走
if (direction == 1) {
// 假如我在最后一列,那么下一个头就是 row+1,col不变;
// 假如我不在最后一列,那么下一个头就是 col+1, row不变
nodeRow += (nodeCol == totalCol - 1 ? 1 : 0) ; // nodeCol == totalCol - 1 => 我在最后一列
nodeCol += (nodeCol < totalCol - 1 ? 1 : 0); // nodeCol < totalCol - 1 => 我不在最后一列
} else { // 正在向下走
// 假如我在最后一行,那么下一个头就是 col+1,row不变;
// 假如我不在最后一行,那么下一个头就是 row+1, col不变
nodeCol += (nodeRow == totalRow - 1 ? 1 : 0); // nodeRow == totalRow - 1 => 我在最后一行
nodeRow += (nodeRow < totalRow - 1 ? 1 : 0); // nodeRow < totalRow - 1 => 我不在最后一行
}
// 转向
direction = 1 - direction;
} else { // 继续沿着当前道路走
nodeRow = new_row;
nodeCol = new_column;
}
}
return result;
}
}
参考 2
【每日一题:小 Fu 讲解】LeetCode 498. Diagonal Traverse - YouTube
这个 YouTube 视频里面提供了另一个思路,把每个对角线看作一次 scan,从 0 开始,奇数次 scan = go down,偶数次 scan = go up。
每个矩形的对角线数量 = col + row - 1
这个解法看起来比较难理解 o(╥﹏╥)o,所以大家有兴趣可以看看。